Triangles

Congruent Figures:

Congruent figures are the figures whose shapes and sizes are same.

 

 

Congruent Triangles:

The triangles which can overlap each other perfectly are called congruent triangles.

For congruent triangles corresponding parts are equal.

If two triangles $\text{ABC}$ and $\text{PQR}$ are congruent, we write as $\Delta \text{ABC}\cong \Delta \text{PQR}$

And we will have

$\angle \text{A}\cong \angle \text{P}$,

$\angle \text{B}\cong \angle \text{Q}$,

$\angle \text{C}\cong \angle \text{R}$

And side $\text{AB}$ $\cong$ side $\text{PQ}$

side $\text{BC}$ $\cong$ side $\text{QR}$

side $\text{AC}$ $\cong$ side $\text{PR}$.

 

 

Criteria for congruency:

 

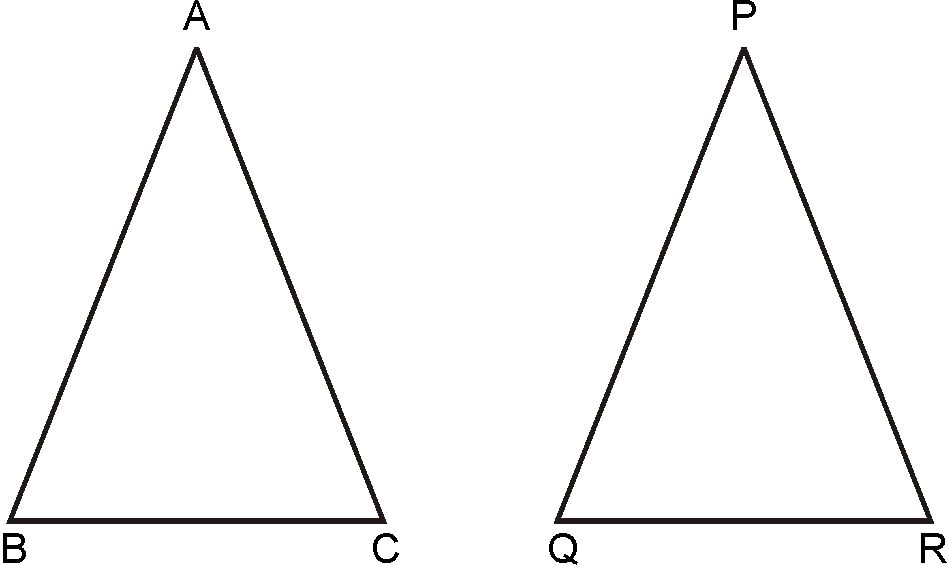
SAS criterion: Triangles are congruent if two sides and included angle of one Triangle are equal to the

sides and the included angle of other triangle.

 

 

 

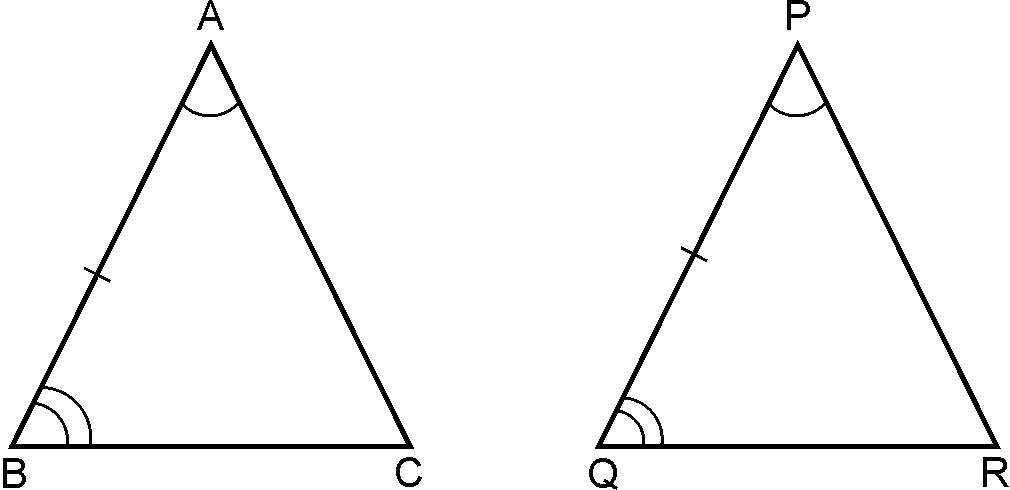
ASA criterion: Two Triangles are congruent if two angles and the included side of one triangle are equal

to two angles and the included side of other triangle.

 

 

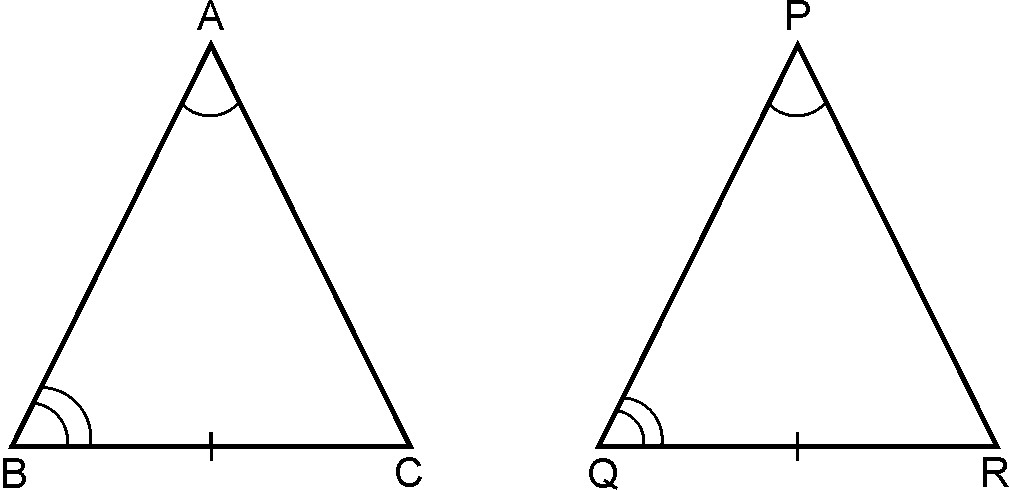
AAS criterion:Two Triangles are congruent if any two pairs of angles and one pair of corresponding

sides are equal.

 

 

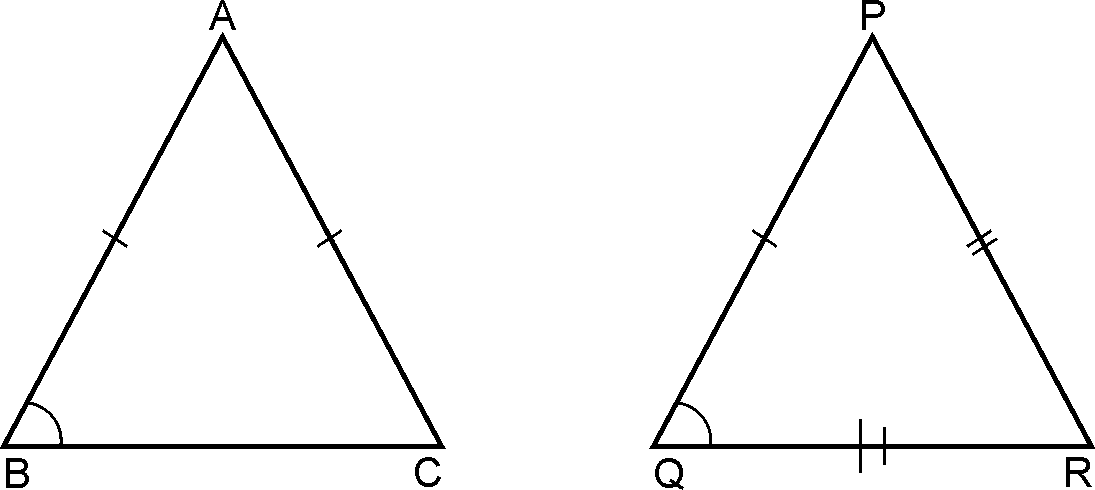
SSS criterion: If three sides of one triangle are equal to three sides of another triangle, then two

triangles are congruent.

 

 

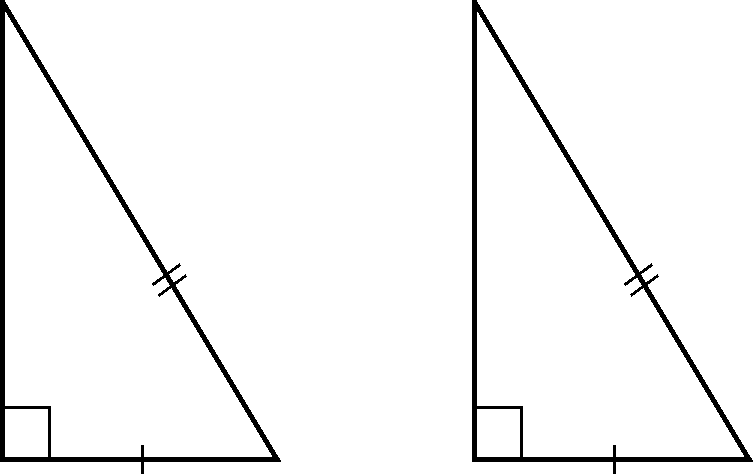
RHS theorem:

If in two right triangles the hypotenuse and one side of one triangle are equal to the hypotenuse and

one side of other triangle, then the two triangles are congruent

 

 

 

Properties of triangle:

Theorem 1:

Angles opposite to equal sides of an isosceles triangle are equal.

 

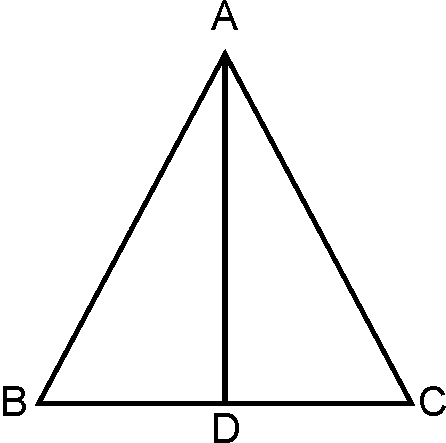
Given: $\Delta \text{ABC}$ is isosceles triangle with

$\text{AB = AC}$

To prove: $\text{B = C}$

Construction: $\text{AD}$ is bisector of angle $\text{A}$

Proof:

$\text{AB = AC}$ ….( Given)

$\angle BA\text{D = }\angle CAD$ (By construction)

$\text{AD = AD}$ common

$\therefore \Delta \text{BAD}\cong \Delta \text{CAD}$ (SAS rule)

$\therefore \angle \text{ABD = }\angle \text{ACD}$ (CPCT)

 

 

 

Theorem 2:

The sides opposite to equal angles are equal

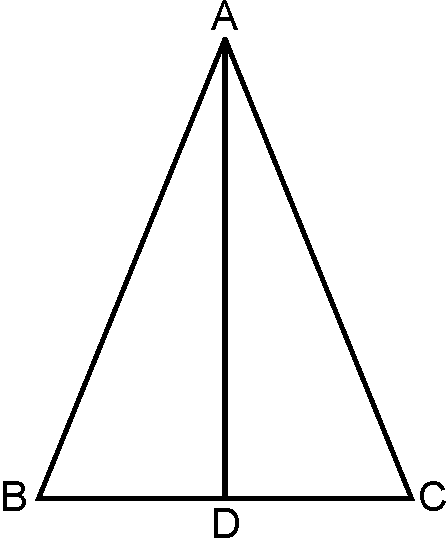
Given: $\Delta \text{ABC}$ is triangle with

$\angle \text{B = }\angle \text{C}$

To prove: $\text{AB = AC}$

Construction: $\text{AD}$ is bisector of angle $\text{A}$ Proof:

$\angle \text{B = }\angle \text{C}$ …(Given )

$\angle BAD\text{ = }\angle CAD$ …. (By construction)

$\text{AD = AD}$ ….. (Common)

$\Delta \text{BAD}\cong \Delta \text{CAD}$ (AAS rule)

$\therefore \text{AB = AC}$ (CPCT)

 

 

Inequality in a triangle:

Theorem 3: If two sides of a triangle are unequal, the longer side has greater angle opposite to it.

Given: $\text{AC > AB}$

To prove :

$\angle \text{B > }\angle \text{C}$

Construction:Take point D on the side AC so that $\text{AB = AD}$

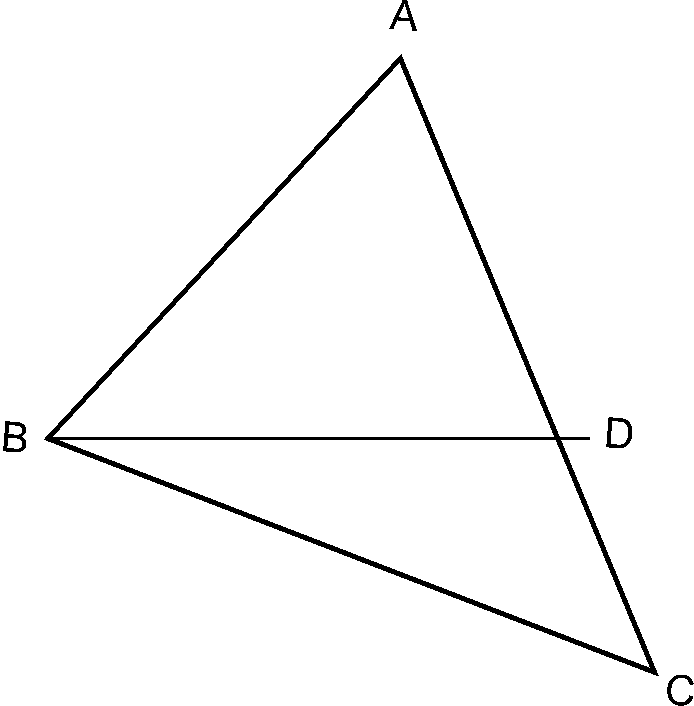
Proof:

As $\text{AB = AD}$

ABD is isosceles triangle.

$\angle \text{ABD = }\angle \text{ADB}$ ….(By isosceles triangle property)..…1

But $\angle \text{ADB}$ is exterior angle of $\text{BDC}$

$\angle \text{ADB > }\angle \text{C}$ ….. (Exterior angle is greater than remote interior angle.)……………2

By $\text{1}$ and $\text{2}$

$\angle \text{ABD > }\angle \text{C}$

But $\angle \text{ABC > }\angle \text{ABD > }\angle \text{C}$ …. (From the figure)

$\therefore \angle \text{ABC > }\angle \text{C}$

 

 

 

Theorem 4:Converse of the theorem:

In a triangle the greater angle has longer side opposite to it.

Given: In $\Delta \text{ABC}$

$\angle \text{ABC > }\angle \text{ACB}$

To prove :

$\text{AC > AB}$

Proof:There are 3 cases

Case i: $\text{AC = AB}$

Case ii: $\text{AC < AB}$

Case iii: $\text{AC > AB}$.

Case i

$\text{AC = AB}$

$\Rightarrow \angle \text{ABC = }\angle \text{ACB}$ (Angles opposite to equal sides)

This is contradiction

Since $\angle \text{ABC > }\angle \text{ACB}$

So $\text{AC}\ne \text{AB}$

Case 2) $\text{AC < AB}$

$\angle \text{ABC < }\angle \text{ACB}$ (Angle opposite to greater side)

contradicts to $\angle \text{ABC > }\angle \text{ACB}$

So, $\text{AC}$ $\text{AB}$

$\therefore$ $\text{AC > AB}$

 

 

 

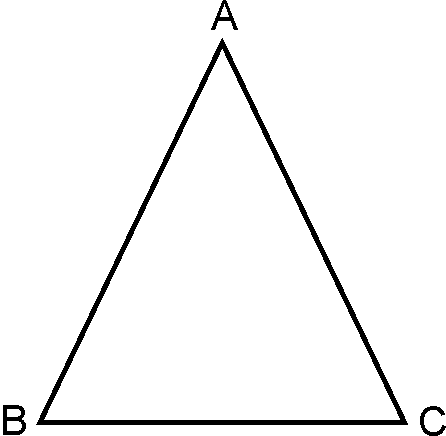
Theorem 5:

The sum of any two sides of a triangle is greater than the third side.

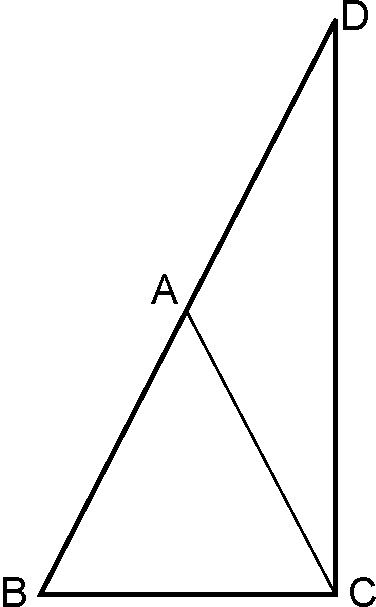
Given: $\Delta \text{ABC}$

To prove:

1) $\text{AB + BC > AC}$

2) $\text{AB + AC > BC}$

3) $\text{AC + BC > AC}$

Construction: Produce $\text{BA}$ to $\text{D}$ such that $\text{AD = AC}$ Join $\text{CD}$.

Proof:

In $\Delta \text{ACD}$, we have $\text{AD = AC}$..(By construction)

$\angle \text{ADC = }\angle \text{ACD}$ … (Angles opposite to equal sides)

$\angle \text{BCA + }\angle \text{ACD > }\angle \text{ADC}$ … (From the fig.)

$\therefore \angle \text{BCD >> }\angle \text{ADC}$

$\text{BD > BC}$ ……….. (Side opposite to larger angle)

$\text{BA + BD > BC}$

$\text{BA + AC > BC}$.

Similarly, we can prove other two inequalities.

 

 

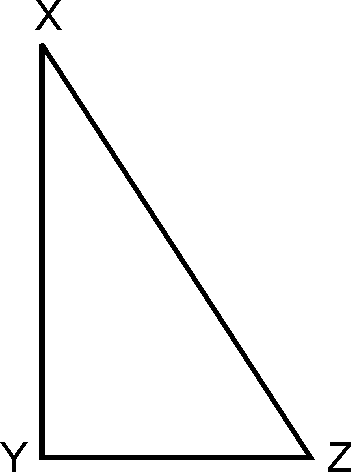
Theorem6 :

In the right angle triangle, the hypotenuse is the longest side.

Given:

$\Delta \text{XYZ}$, $\angle \text{Y = 90°}$.

To prove: $\text{XZ}$ is largest side

i.e. $\text{XZ > XY}$ and $\text{XZ > YZ}$.

Proof:

$\text{x + y + z = 180°}$ (Angle sum property of triangle)

$\text{x + 90}°\text{ + z = 180°}$

$\text{X + Z = 90°}$.

$\Rightarrow$ $\text{X}$ and $\text{ Z}$ are acute angles

$\Rightarrow$ $\text{X < 90°}$, $\text{Z < 90°}$

$\therefore \text{YZ < XZ, XY < XZ}$.(Sides opposite to greater angles)

$\therefore \text{XZ}$ is largest side.