Lines and Angles

Collinear points:

If three or more points lie on same line they are called collinear points.

 

 

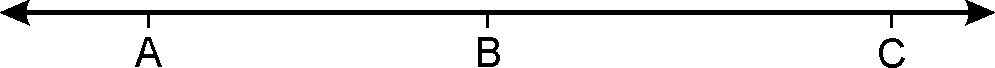
Angle: Angle is forms when two rays originate from same endpoint.

 

 

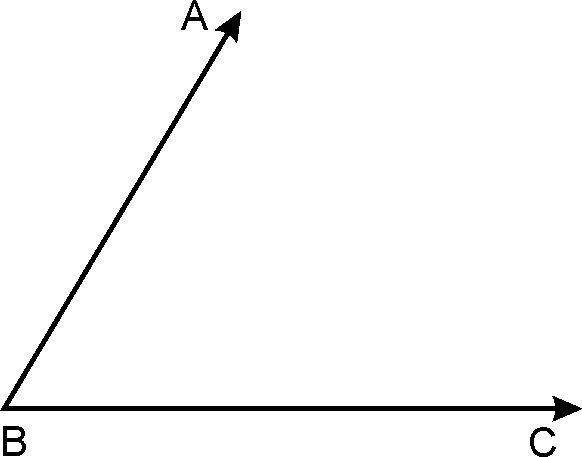
Vertex: The end point of angle is called vertex.

 

 

Arms: The rays making an angle are called the arms.

 

 

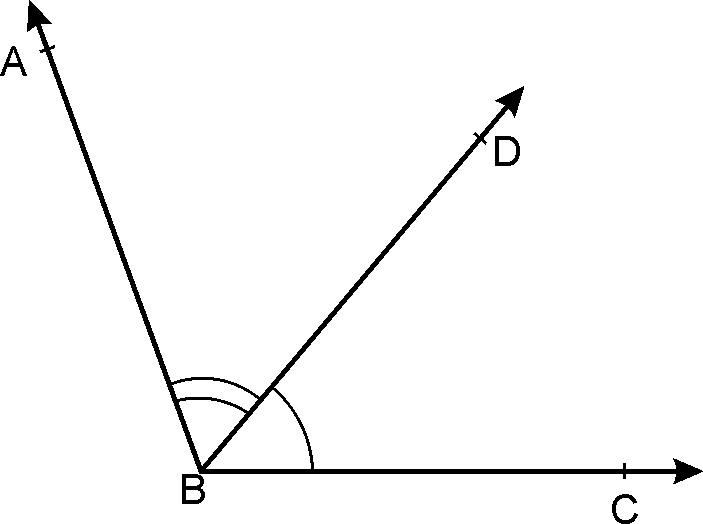
Adjacent angles:

Two angles are called adjacent angles if they have a common vertex, a common arm, and non-common arms are on different sides of the common arms.

 

 

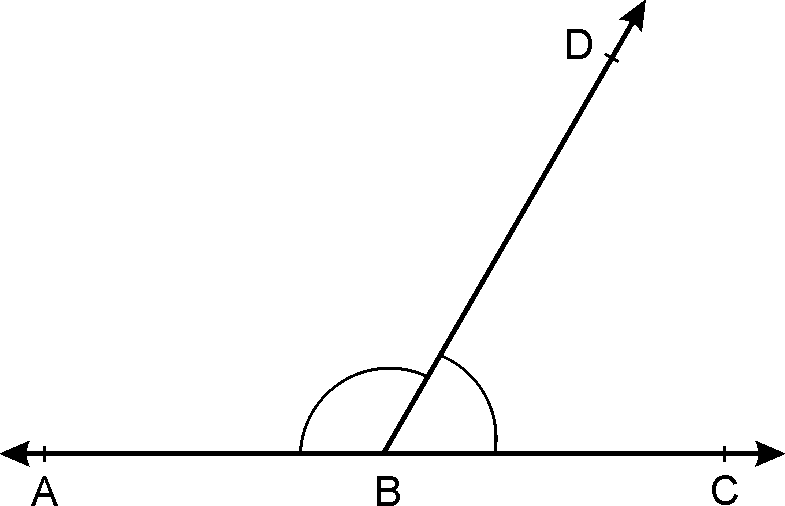
Linear pair angles:

If for adjacent angles, the non common pair rays form a line, then angles so formed are

called angles of linear pair.

 

 

Linear pair Axiom:

i)If a ray stands on a line, then sum of two adjacent angles so formed is ${180}^0$.

ii)If the sum of two adjacent angles ${180}^0$ ,then a ray stands on a line.

 

 

Vertically Opposite angles :

When two lines AB and CD intersect each other, $\angle AOC$ and $\angle BOD$ are called vertically opposite

angles.

 

 

 

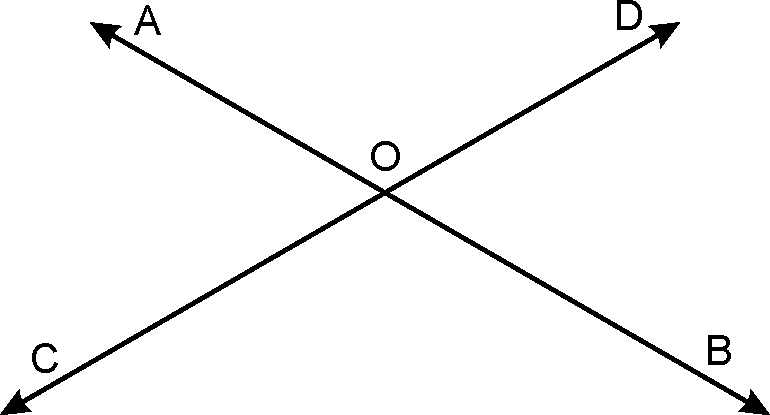
Theorem:

If two lines intersect each other, then the verically opposite angles angles are equal.

Given: AB, CD are two lines which intersect at point O.

 

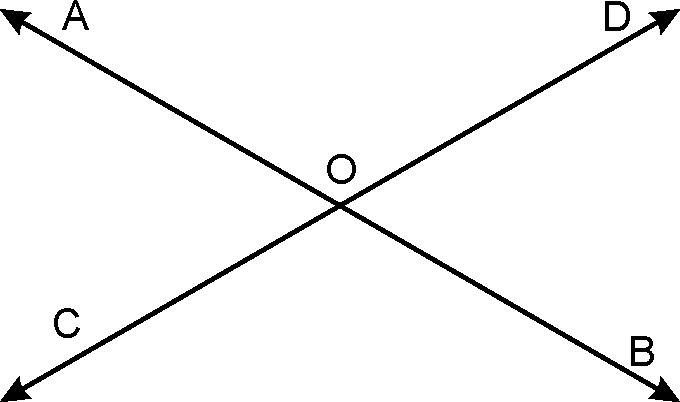
To prove:
$\angle AOC=\angle BOD$

$\angle AOD=\angle BOC$

Proof:

$\angle AOC+\angle AOD={180}^{°}$ (Linear pair axiom)….1

$\angle AOD+\angle BOD={180}^{°}$ (Linear pair axiom)….2

Adding st. 1 and st. 2

$\angle AOC+\angle AOD=\angle AOD+\angle BOD$ (From 1 and 2)

$\angle AOC+\angle BOD$ Proved.

Similarly, we can prove

$\angle AOD=\angle BOC$

Parallel lines and transversal:

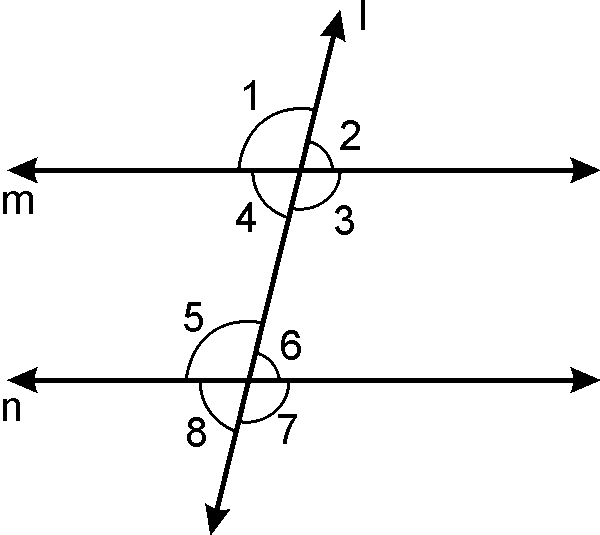
1) Corresponding angles: When a transversal intersects two parallel lines, Corresponding angles are angles which lie on same side of transversal and both lie above or below the two lines.

1) $\angle 1$ and $\angle 5$
2) $\angle 2$ and $\angle 6$
3) $\angle 4$ and $\angle 8$
4) $\angle 3$ and $\angle 7$

2) Alternate angles:

1) $\angle 4$ and $\angle 6$
2) $\angle 3$ and $\angle 5$

3) Interior angles:

1) $\angle 4$ and $\angle 5$
2) $\angle 3$ and $\angle 6$

 

 

Corresponding angle axiom:

1) If a transversal intersects two parallel lines, then each pair of corresponding angles equal.

2) If a transversal intersects two lines such that a pair of corresponding angles is equal, then two lines are parallel to each other.

 

 

Theorem: If a transversal intersects two parallel lines then, each pair of alternate angle is equal.

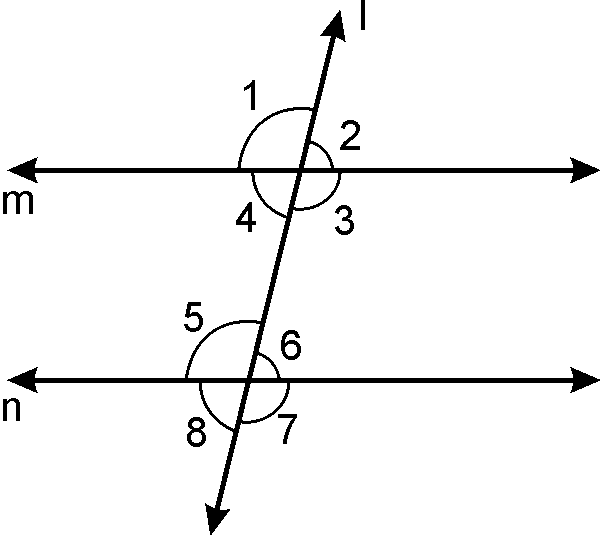
Given:

$AB\parallel CD$ , $PQ$ is transversal.

To prove:

$\angle 4\cong \angle 6$ or $\angle AST\cong \angle STD$

$\angle 3\cong \angle 5$ or $\angle BST\cong \angle STC$

Proof :
$\angle 1\cong \angle 5$ or $\angle PSA\cong \angle STC$ (By corresponding axiom).(1)

But $\angle 1\cong \angle 3$ or $\angle PSA\cong \angle BST$ (Vertically opposite angle)….(2)

$\angle 5\cong \angle 3$ or $\angle STC\cong \angle BST$ (From 1 and 2).

Proved.

 

 

 

Theorem 2:

If a transversal intersects two Parallel Lines then each pair of interior angles on the same

side of transversal is supplementary.

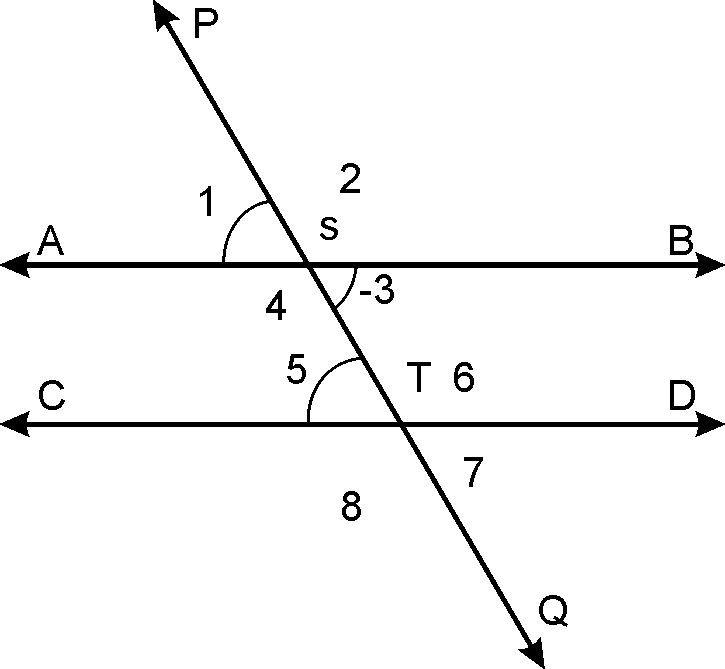
Given:

$AB\parallel CD$ , $PQ$ is transversal.

To prove :

$\angle 5+\angle 4={180}^{°}$ or $\angle STC+\angle AST={180}^{°}$ And

$\angle 3+\angle 6={180}^{°}$ or $\angle BST+\angle STD={180}^{°}$

Proof:

$\angle 3\cong \angle 5$ (Alternate angle theorem)….1

But

$\angle 3+\angle 4=180$ (Linear pair)……..2

$\angle 5+\angle 4={180}^{°}$ (From 1 and 2)

Or $\angle STC+\angle AST={180}^{°}$

Hence proved.

Similarly, we can prove

$\angle BST+\angle STD={180}^{°}$

 

 

 

Theorem 3: Converse of the theorem:

If a transversal intersects two lines such that a pair of angles on the same side of

transversal is supplementary then two lines are parallel.

 

 

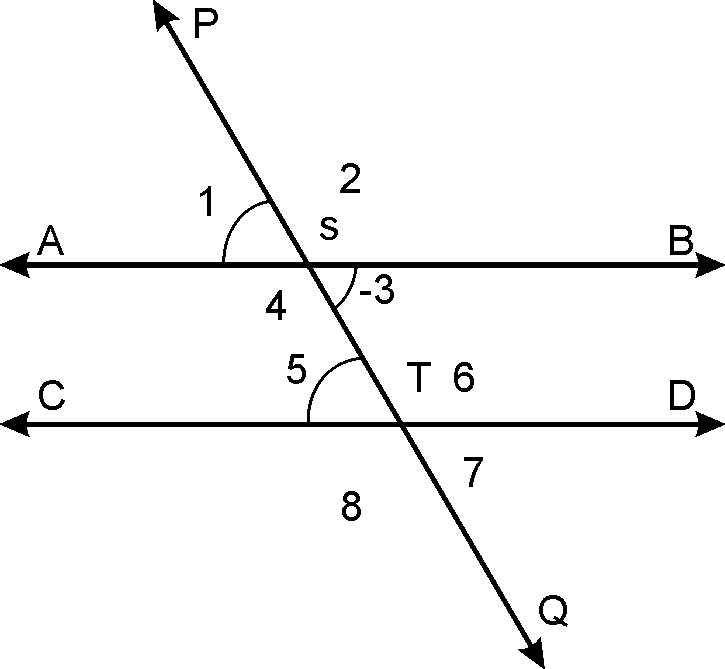
Given:

Lines AB and {CD, PQ} is transversal.

$\angle AST+\angle STC={180}^{°}.$

To prove :

AB is parallel to CD.

Proof:

$\angle AST+\angle STC={180}^{°}$ (Given)…1

$\angle STC+\angle CTQ={180}^{°}$ (Linear pair)….2

$\angle AST+\angle STC=\angle STC+\angle CTQ$

$\angle AST=\angle CTQ$

$ABisparallelCD$ (By corresponding angle axiom).

 

 

 

Theorem 4:

Lines which are parallel to same line are parallel to each other.

 

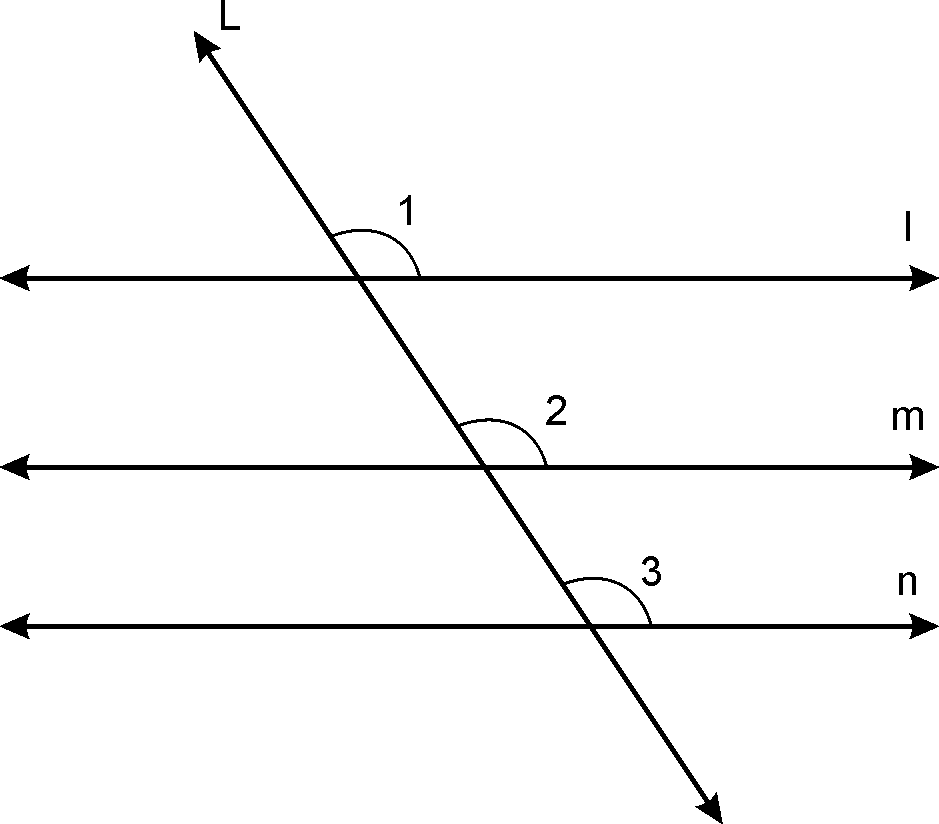
Given:

Line $l\parallel$ line $m$
Line $l\parallel$ line $n$

To prove:

Line $n\parallel$ line $m$

Proof:

Line $l\parallel$ line $m$

$\angle 1\cong \angle 2$ (Corresponding angle axiom)…..1

Line $l\parallel$ line $n$

$\angle 1\cong \angle 3$ (Corresponding angle axiom)…2

$\angle 2\cong \angle 3$ (From 1 and 2)

Line $m\parallel$ line $n$ (Corresponding angle axiom).

 

 

 

Theorem 5:

If two parallel lines are intersected by a transversal bisectors of any pair of alternate interior angles are parallel.

[A1] 

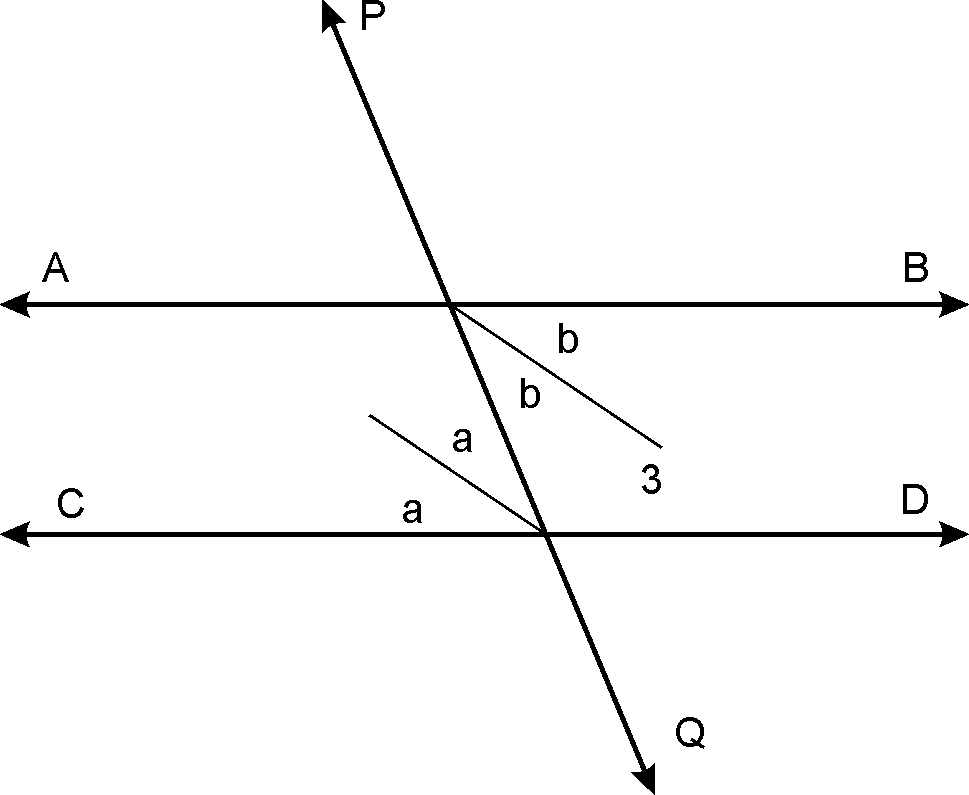
Given:

$AB\parallel CD$

PQ is transversal.
MT is bisector of $\angle STC.$

NS is bisector of $\angle TSB.$

To prove: MT $\parallel$ NS

Proof: Let

$\angle CTM=\angle MTS=a$

$\angle TSN=\angle NSB=b$

$\angle STC=\angle TSB$ (Alternate angles)

$2a=2b$

$a=b$

$\angle STM=\angle BST.$

$BS\parallel TM$ (By alternate angle theorem)

 

 

 

Theorem 6 :Angle sum property

The sum of the angles of a triangle is ${180}^{°}.$

 

Given: in

$\Delta PQR,\angle P,\angle Q,\angle Rarex,y,z.$

To prove: $x+y+z={180}^{°}$

Construction: Draw line parallel to QR passing through P

Proof:

$a+b+x={180}^{°}$ (Linear angles)…(1)

If PQ is transversal,

$a=y$ (Alternate angles)…(2)

PR is transversal,

$b=z$ (Alternate angles)…(3)

From 1, 2 and 3

$y+x+z={180}^{°}{}^{°}$

 

 

 

 

Theorem 7: Exterior angle theorem:

If a side of a triangle is produced, then the exterior angle so formed is equal to the sum of two interior opposite angles.

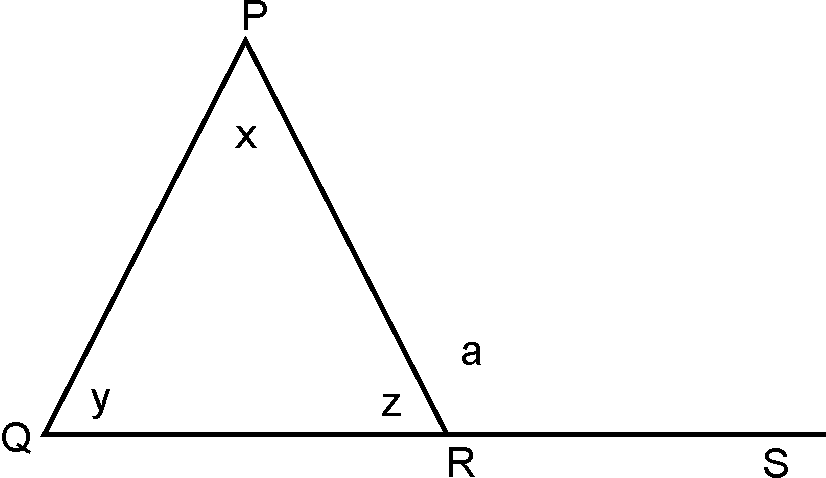
Given:

$in\Delta PQR,\angle P,\angle Q,\angle Rarex,y,z.$

And $\angle PRS=a$

To prove: $a=x+y$

Proof: $x+y+x={180}^{°}$

(By angle sum property of triangle)…1

$a+z={180}^{°}$ (Linear pair)…2

$x+y+z=a+z$ (From 1 and 2)

$x+y=a.$