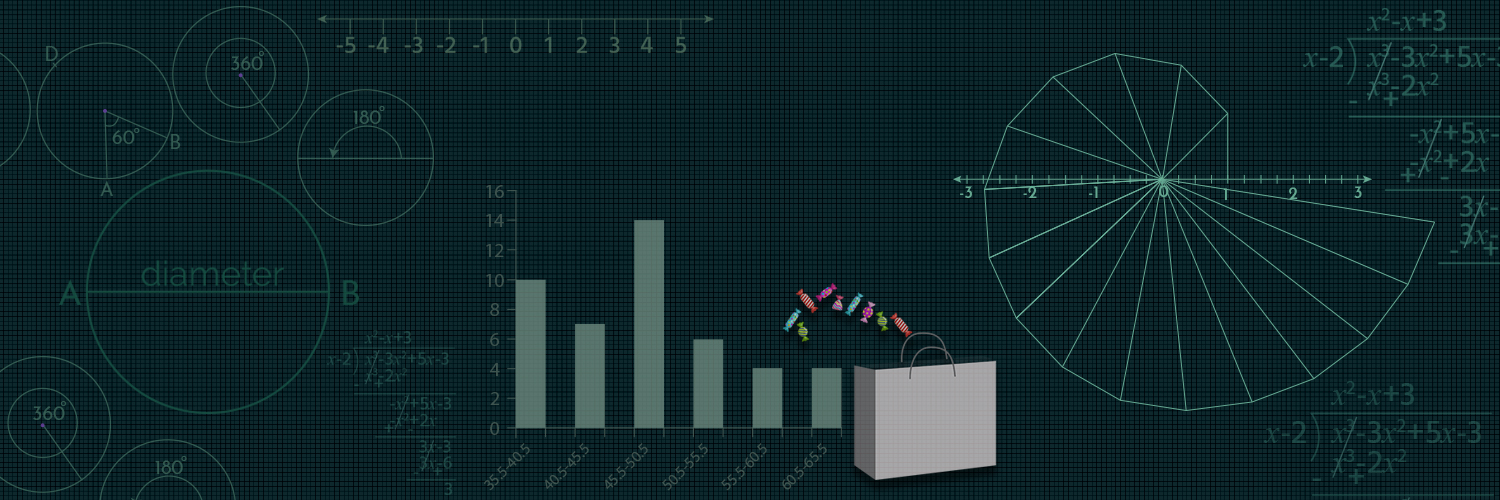
Theorem 1 -Angle sum property of
Quadrilateral:
The sum of four angles of a Quadrilateral is

Given: A Quadrilateral .
To prove :
Construction: Join AC
Proof: In
(By angle sum
property of triangle)
In
(By angle sum property of
triangle)
So, adding
Remarks:
·
A parallelogram
is a trapezium. But a trapezium is not parallelogram.
·
A rectangle is
parallelogram, But a parallelogram is not a rectangle.
·
A rhombus is
parallelogram, but parallelogram is not a rhombus.
·
A square is
parallelogram, rectangle, rhombus but not viceversa.
·
A kite is not a parallelogram.
Properties of parallelogram:
A Quadrilateral is parallelogram if both
the pairs of opposite sides are parallel.
Theorem 2:
A diagonal of a parallelogram divides it
into two congruent triangles.
Given:
is
parallelogram. is
diagonal

To prove:
Proof:
And is transversal
So
…..(Alternate
angles)
and is transversal
……(Alternate
angles)
…(Common)
…( By ASA rule.)
Theorem 3:
In a parallelogram, opposite sides are equal
and opposite angles are equal.
Given :
is
parallelogram

To prove:
and
Construction: Join AC
Proof:
And is transversal
…..(Alternate
angles)
and AC is
transversal
……(Alternate
angles)
…(Common)
(By ASA
rule.)
(CPCT).
Similarly it can be proved that
Theorem 4:
The
diagonals of a parallelogrambisect each other.
Given: is a
parallelogram

Ac
and intersect at .
To prove:
is
midpoint of and BD.
That is
Proof:
In and
….(
Alternate angles, ,BD as transversal)
…. (
Alternate angles, ,AC as
transversal)
……
(Opp sides of parallelogram)
…..(By ASA
rule.)
So (CPCT)
Theorem 5:
A Quadrilateral is parallelograms if
opposite sides are congruent.
Given:
is
Quadrilateral
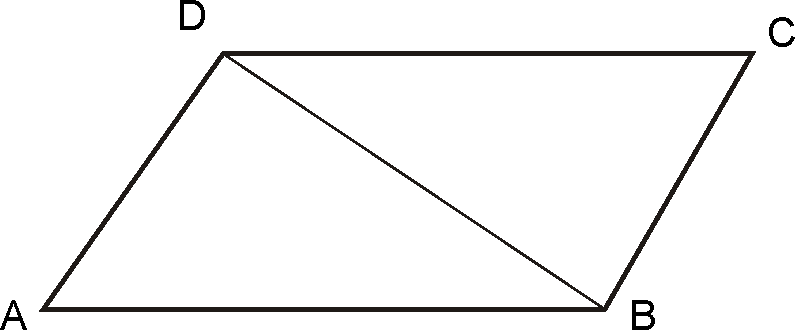
With
and
To prove: ABCD
is parallelogram
i.e.
Construction:Join
Proof:
In and
….(Given)
….(Given)
…(Common)
….(SSS rule)
….. (CPCT)
…..(Alternate
angle test)
Similarly
(CPCT)
…(Alternate
angle test)
AS
both the pair of opposite sides areparallel, we say is
parallelogram.
Theorem 6:
A
Quadrilateral is parallelogram if opposite angles are congruent.
Given:
is
Quadrilateral
With
and

To prove: is
parallelogram
i.e.
Construction : Join
Proof:
So …(1)
But we know
(Angle sum property of
quadrilateral)…2
(From and
)
( Sum of
interior angle criteria)
Similarly,
can be
proved.
As both the pair of sides are parallel,
we say is
parallelogram.
Theorem 7:
A Quadrilateral is parallelogram if a
pair of opposite sides is congruent and parallel.
Given:
is
quadrilateral.
To prove: ABCD is parallelogram.
i.e.
Proof:

Construction: join AC
Proof:
In and
…(Given)
…(Alternate
angle as )
…..(Common)
… (SAS rule)
So ….( CPCT)
(Alternate angle
criteria)
Converse
:
Theorem 8 : If diagonals of parallelogram are equal
then it is rectangle.
Given:
is
parallelogram
be
its diagonal.
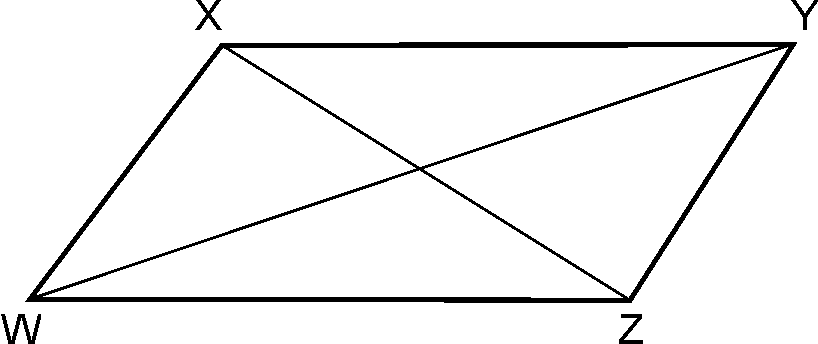
To prove: is
rectangle
i.e.
Proof:
In and
….(Given)
….(Opp.
side of parallelogram)
…(Common)
…(SSS rule)
(CPCT)…..1
But …(Interior angles
are supplementary)
…(From 1)
Similarly we can show all the angles of
quadrilateral are
Hence it is rectangle.
Theorem 9:
Diagonals of a rhombus are perpendicular
to each other.
Given :
is
rhombus.
is
parallelogram.
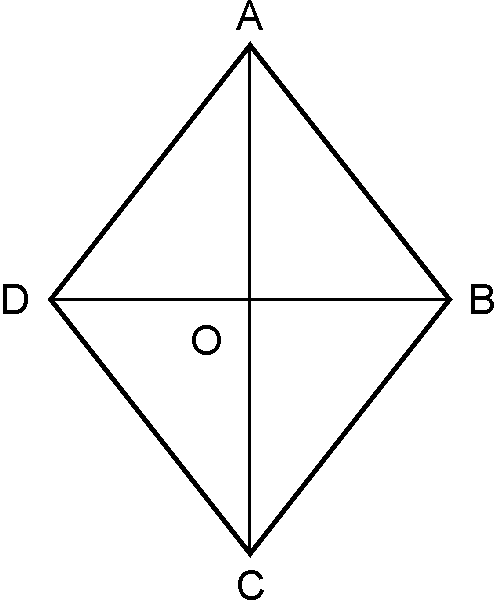
To prove:
Proof:
In and
…
.(Given)
…….
(Diagonals of parallelogram bisect each other)
……..(
Common)
…(SSS test)
So …(CPCT)
But ….(Linear pair)
Theorem 10- Mid-point theorem:
The
line segment joining the midpoint of any two sides of a triangle is parallel to
third side and is half of third side.
Given: In and are
midpoints of the sides and respectively.
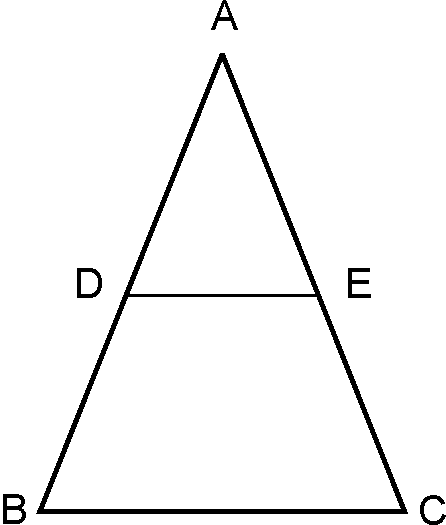
To prove:
1) 2) .
Construction: produce DE so that DE=EF.
Join CF
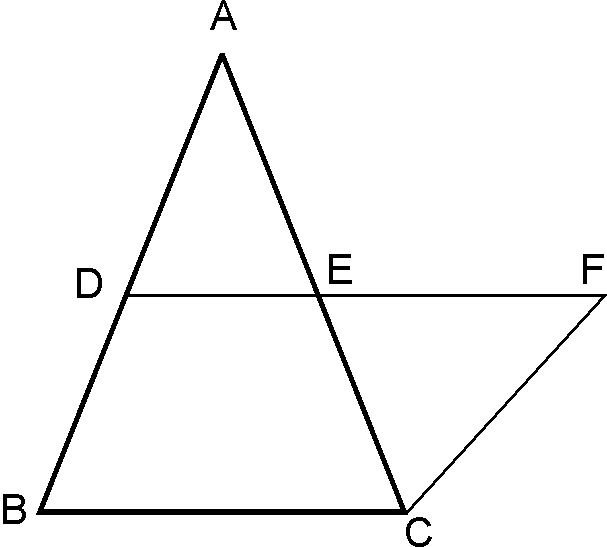
Proof:
In and
…. (E is midpoint of AC)
…..
(By construction)
……(V. opp angles)
…… (SAS rule)
…(CPCT)
……. (CPCT)
But …….(D
is midpoint)
So
…(CPCT)
is parallelogram……
(One pair of side is parallel and equal)
So,
(By
construction)
Theorem 11 -Converse of midpoint theorem:
The
line through the midpoint of one side of a triangle, parallel to other side,
intersects the third side at its midpoint.
Given:
In , is
mid-point of
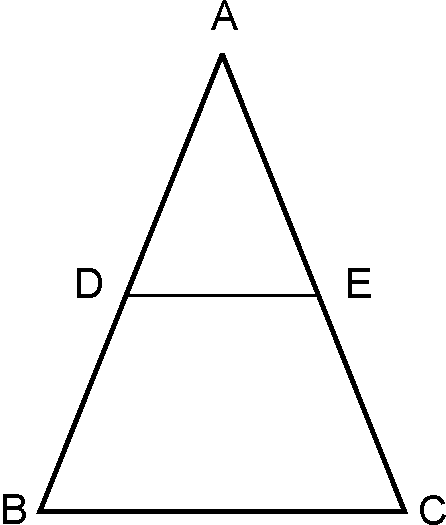
To prove:
is
midpoint of .
Proof:
Suppose is not
midpoint of .
Let ’
is midpoint of .
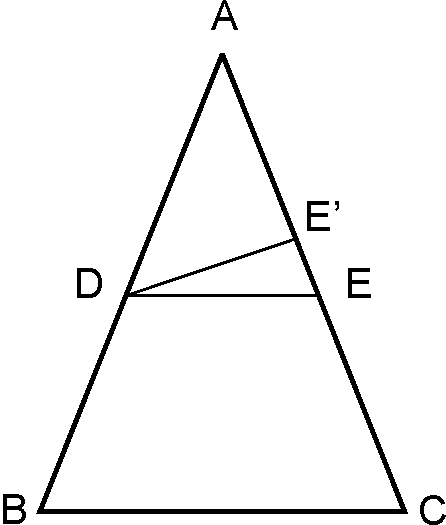
Then By mid-point theorem,
But …….. (Given)
and
’
are two intersecting line are parallel to .
Contradicts the parallel line axiom.
So is mid-point of .