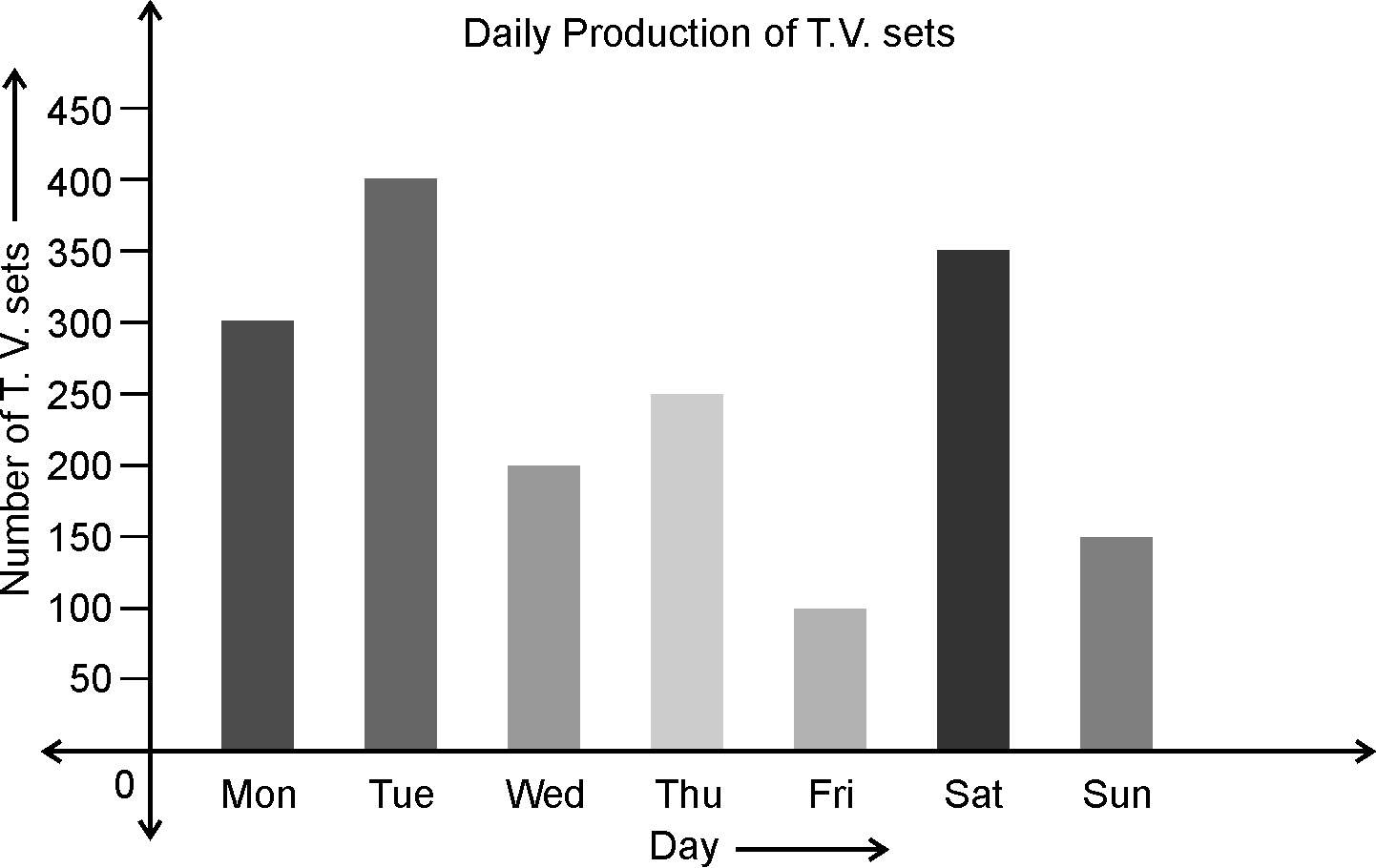Statistics

Data: The information or facts or values which are numerical, collected with definite purpose iscalled data.

e.g.: Record of every day temperature for a month of June of city $\text{ A}$.

Runs scored by cricketer in $\text{10}$ matches.

Statistics:Statistics deals with collection, presentation, and analysis of data.

Types of data:

Primary data: The data collected by investigator personally is called primary data.

Secondary data: The information gathered from a source which already had the record,is called secondary data.

Arrangement of DATA:

Raw data: The data which is not arranged in any way is called raw data.

e.g. The score of cricketer in $\text{5}$ matches

10,20,20,10,30,10,30,10,20,10,20,

Range: Difference between highest and lowest value in data is the range of data.

e.g. For data: $\text{10, 20, 20, 10, 30, 10, 30, 10, 20, 10, 20,}$

Range = highest value-lowest value

$\text{= 30 - 10}$

$\text{= 20}$

Ungrouped frequency table:

Given data: $\text{10, 20, 20, 10, 30, 10, 30, 10, 20, 10, 20}$

The table representing data as following wayis called ungrouped frequency table :

Grouped frequency table:

Given data: $\text{11, 25, 20, 22, 30, 32, 40, 25, 12, 45, 30, 32, 20, 20, 25, 19, 49}$.

The table representing data as following way is called grouped frequency table:

Class Interval:

The grouping of data into small groups is called class interval or classes.

e.g. $\text{11 - 20, 21- 30,}$, etc. are the classes or the data.

Class limits:

Upper class limit: The highest value of class is called upper class limit.

Lower class limit: The lowest value class limit of the class is called lower class limit.

Class width: The difference between upper and lower limit of the class is called class width

or length of class interval.

Inclusive class interval(non overlapping classes): The classes $\text{11 - 20, 21 - 30}$ etc. are non overlapping classes as no class limit overlap with other.

The values included in class $\text{11 - 20}$ are values between $\text{11}$ and $\text{20}$, including $\text{11}$ and $\text{20}$.

Exclusive type class intervals: For the classes $\text{10 - 20, 20 - 30, 30 - 40…}$ etc. the upper class limit of previous class and lower class limit of next class overlap.Such classes are called exclusive classes.

Here the class $\text{10 - 20}$ includes the values less than $\text{20}$, exclude the value $\text{20}$.

The value $\text{20}$ is included in class $\text{20 - 30}$.

Class mark:

Class mark is mid point of the class interval.

It is calculated by

$\text{class mark = }\frac{\text{upper class limit + lower class limit}}{\text{2}}$

Graphs:

1)Bar graphs: Representation of data using bars of equal width and with uniform spacing

between them.The height of bars is in proportion to the frequency.

This is used when all classes are of equal length.

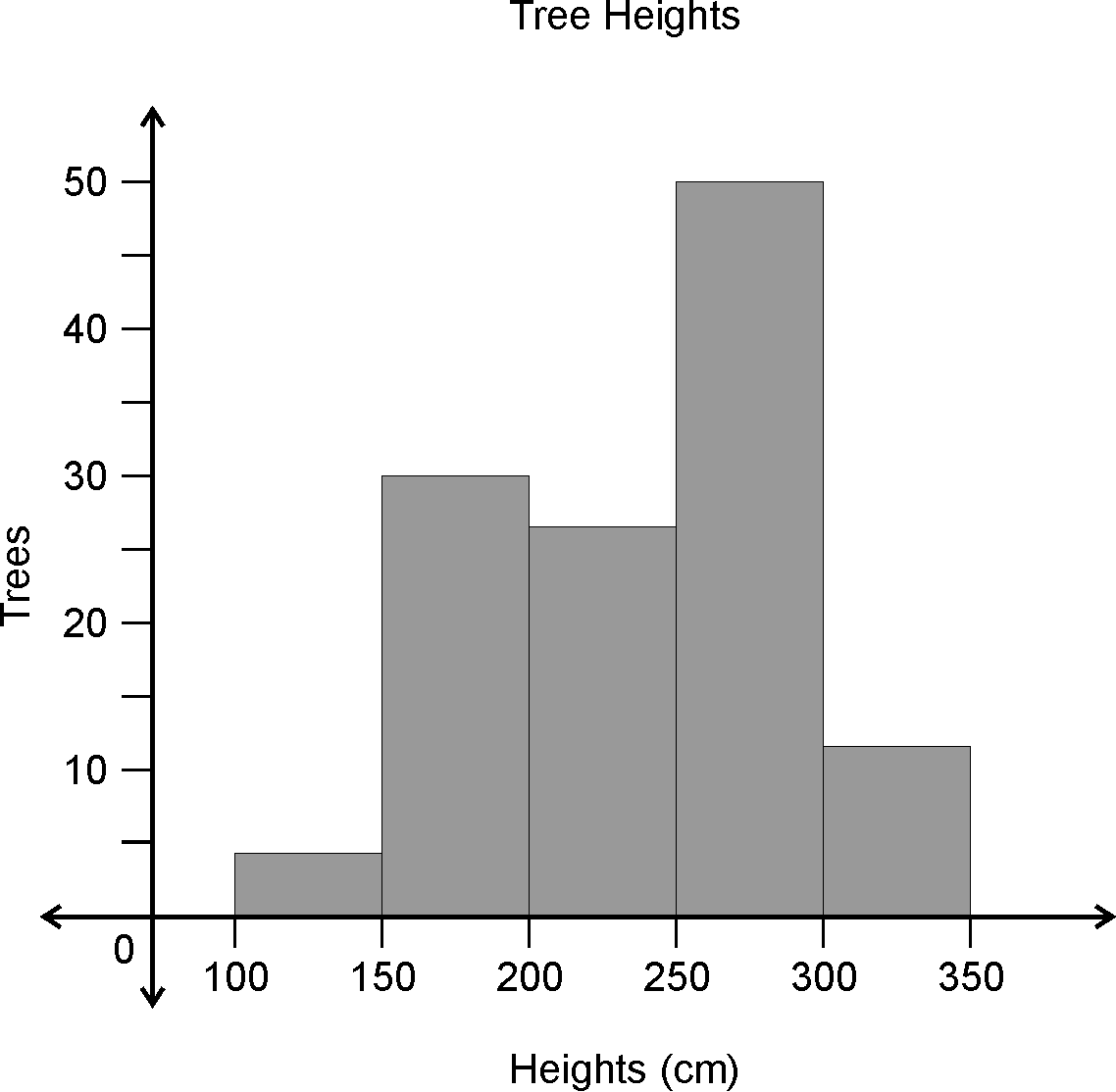
Histogram:

The representation of data with the rectangles,whose breadth is proportional to class-width andlength is proportional to frequency of that class interval

This can be used when we have unequal class interval

Frequency polygon:

When the points with coordinates as (class mark,frequency) are plotted and joined with straight line, the graph so obtained is called the frequency polygon.

Measures of central tendency:

Mean $\left(\overline{\text{x}}\right)$: It is average of data.

i) For ungrouped data, mean $\overline{\text{x}}\text{ = }\frac{\text{sum of all observation}}{\text{total no}\text{.of observation}}\text{ = }\frac{{\displaystyle \sum {\text{x}}_{\text{i}}}}{\text{N}}$

ii) For ungrouped frequency table, mean $\text{= }\overline{\text{x}}\text{ = }\frac{{\displaystyle \sum {\text{f}}_{\text{i}}{\text{x}}_{\text{i}}}}{{\displaystyle \sum {\text{f}}_{\text{i}}}}$

Median:

Median isthe middle value of data when data is arranged in ascending order.

If $\text{N =}$ total number of observations.

i) When $\text{N}$ is odd,

Median $\text{= }{\left(\frac{\text{n + 1}}{\text{2}}\right)}^{\text{th}}$ observation

ii) When $\text{N =}$ even

Median $\text{= }\frac{{\left(\frac{\text{N}}{\text{2}}\right)}^{\text{th}}\text{obs}\text{. + }{\left(\frac{\text{n}}{\text{2}}\text{ + 1}\right)}^{\text{th}}\text{obs}}{\text{2}}$

Mode: It is the value which occurs most frequently or it is the value with highest frequency.