Areas of Parallelogram and Triangles

Theorem 1:

Parallelograms on the same base and between the same parallels are equal in area.

[A1] 

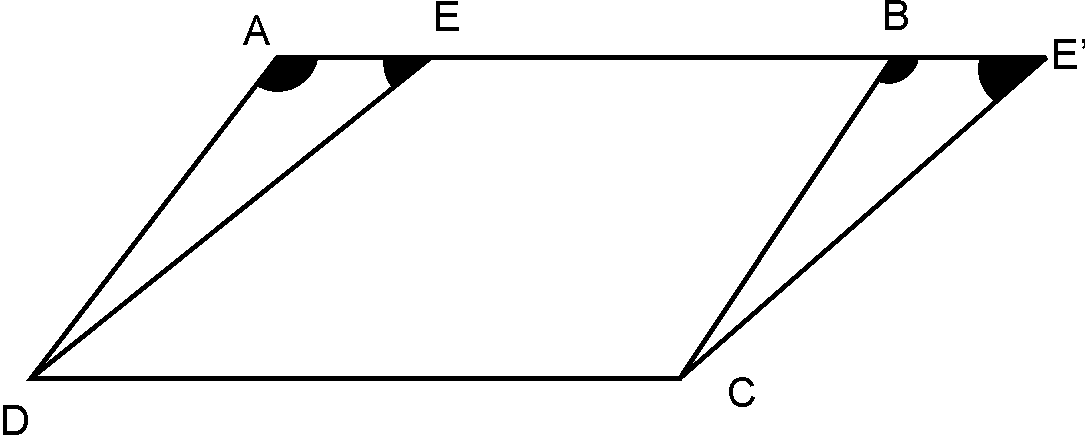
Given:

$\square \text{ABCD}$ and $\square \text{EFCD}$ are two parallelograms.

To prove:

$\text{A}\left(\square \text{ABCD}\right)\text{ = A}\left(\square \text{EFCD}\right)$

Proof :

In $\Delta \text{ADE}$ and $\Delta \text{BCF}$

$\angle \text{DAE = }\angle \text{CBF}$ (Corresponding angles, $\text{AD}\parallel \text{BC}$,and AF transversal.)

$\angle \text{AED = }\angle \text{BFC}$ (Corresponding angles, $\text{DE}\parallel \text{FC}$, and $\text{AF}$ transversal.)

So,

$\angle \text{ADE = }\angle \text{BCF}$ (Third angle of the triangles, by angle sum property)

$\text{AD = BC}$ (Opposite sides of parallelogram $\text{ABCD}$ )

$\Delta \text{ADE}\cong \Delta \text{BCF}$ (ASA rule)

So $\text{A}\left(\text{ΔADE}\right)\text{ = A}\left(\text{ΔBCF}\right)$

$\text{A}\left(\text{ABCD}\right)\text{ = A}\left(\text{ADE}\right)\text{ + A}\left(\text{EDCB}\right)$ (From the fig.)

$\text{= A}\left(\text{ BCF}\right)\text{ + A}\left(\text{EDCB}\right)$

$\therefore \text{A}\left(\text{ABCD}\right)\text{ = A}\left(\text{EFCD}\right)$.

Theorem 2: Area of triangle is half of parallelogram with common base and between same parallel.

Given:

Let $\Delta \text{ABC}$ and parallelogram $\text{BCED}$ be with common base $\text{BC}$.

$\mathrm{BC}\parallel ED$

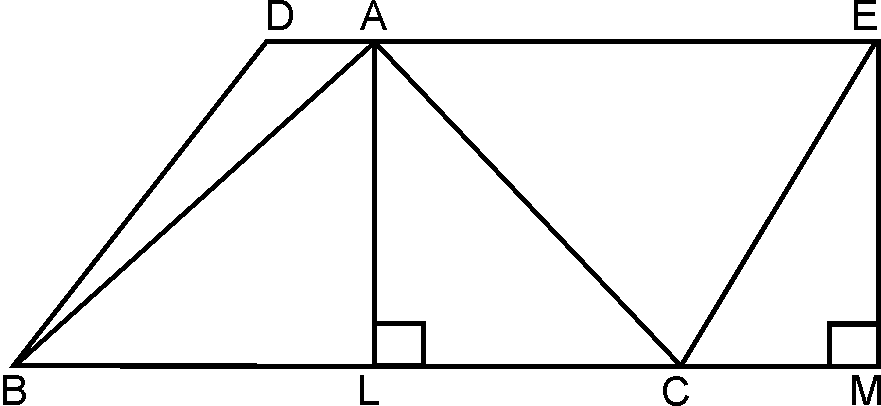
To prove :

$\left(\Delta \text{ABC}\right)\text{ =}\frac{1}{2}\text{ A}\left(\square \text{BCED}\right)$

Construction: Draw $\text{AL}\perp \text{BC}$, $\text{EM}\perp \text{BC}$.

Extend $\text{BC}$ Up to $\text{M}$.

Proof:

AS $\text{BC}\parallel \text{DE}$,

$\text{AL = ME}$ (Distance between two parallel lines is equal)

Now, $\text{A}\left(\Delta \text{ABC}\right)\text{ = }\frac{\text{1}}{\text{2}}\left(\text{BC × AL}\right)$

$\text{A}\left(\Delta \text{ABC}\right)\text{ = }\frac{\text{1}}{\text{2}}\left(\text{BC × ME}\right)$

$\text{= }\frac{\text{1}}{\text{2}}\text{A}\left(\square \text{BCDE}\right)$.

Theorem 3: Two triangles on the same base (or equal bases) and between the same parallels are equal in area.

Given:

$\Delta \text{ABC}$ And $\Delta \text{PBC}$ be two triangles with common base $\text{BC}$ and between same

Parallel lines

$\text{BC}\parallel \text{AP}$

To prove:

$\text{A}\left(\Delta \text{ABC}\right)\text{ = A}\left(\Delta \text{PBC}\right)$

Construction: Draw $\text{BD}\parallel \text{CA}$, and $\text{CQ}\parallel \text{BP}$,

Let line $\text{AP}$ meets $\text{BD}$ at $\text{D}$ and $\text{CQ}$ at $\text{Q}$.

Proof:

$\text{A}\left(\Delta \text{ABC}\right)\text{ = }\frac{1}{2}\text{A}\left(\square \text{BCAD}\right)$ (Triangle and parallel gram with common base and

Between parallel lines) …(1)

And $\text{A}\left(\Delta \text{PBC}\right)\text{ = }\frac{1}{2}\text{A}\left(\square \text{BCQP}\right)$ …(2)

$\square \text{BCAD}$ is parallelogram

$\square \text{BCQP}$ is parallelogram.

Both the parallelogram have same base and between two parallel lines,

$\therefore \text{A}\left(\square \text{BCAD}\right)\text{ = A}\left(\square \text{BCQP}\right)$ ….(3)

So, $\text{A}\left(\Delta \text{ABC}\right)\text{ = A}\left(\Delta \text{PBC}\right)$ (from $\text{1, 2}$ and $\text{3}$ )

Theorem 4 : Two triangles having the same base and equal areas lie between the same

Parallels.

Given:

$\Delta \text{ABC}$ and $\Delta PBC$ have equal base BC.

$\text{A}\left(\Delta \text{ABC}\right)\text{ = A}\left(\Delta \text{PBC}\right)$,

Let $\text{AN}\perp \text{BC}$, $\text{PM}\perp \text{BC}$

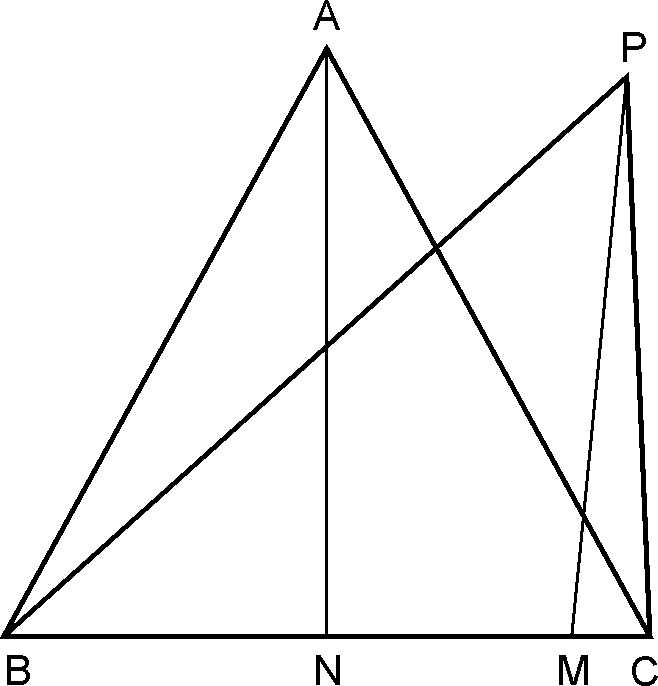
To prove:

Triangles lie between two parallel lines.

i.e. $\text{AN = PM}$

Proof :

$\text{A}\left(\Delta \text{ABC}\right)\text{ = }\frac{\text{1}}{\text{2}}\text{BC }\times \text{ AN}$

$\text{A}\left(\Delta \text{PBC}\right)\text{ = }\frac{\text{1}}{\text{2}}\text{BC }\times \text{ PM}$

As $\text{A}\left(\Delta \text{ABC}\right)\text{ = A}\left(\Delta \text{PBC}\right)$

$\frac{\text{1}}{\text{2}}\text{BC }\times \text{ AN = }\frac{\text{1}}{\text{2}}\text{BC }\times \text{ PM}$

$\therefore \text{AN = PM}$

AS corresponding heights are equal, we say point $\text{A}$ and $\text{P}$ lie on the line parallel

to $\text{BC}$, through $\text{A}$.

Hence the result.