Circles

Tutormate > CBSE Syllabus-Class 9th Maths > Circles

10 Circles

CIRCLES

Circle :

A circle is the collection of all the points which are at a fixed distance from a fixed
point in a plane.

Centre:

The fixed point is called centre of the circle.

Radius(r):

The fixed distance is called the radius of the circle.

Interior region of circle:

It is the part of plane which is within the circle.

The distance between any point in interior region and centre is less than
the radius of the circle.

Exterior region of the circle:

The part of plane which is out side the circle.

The distance between any point in exterior region and centre is
greater than the radius of the circle.

Chord :

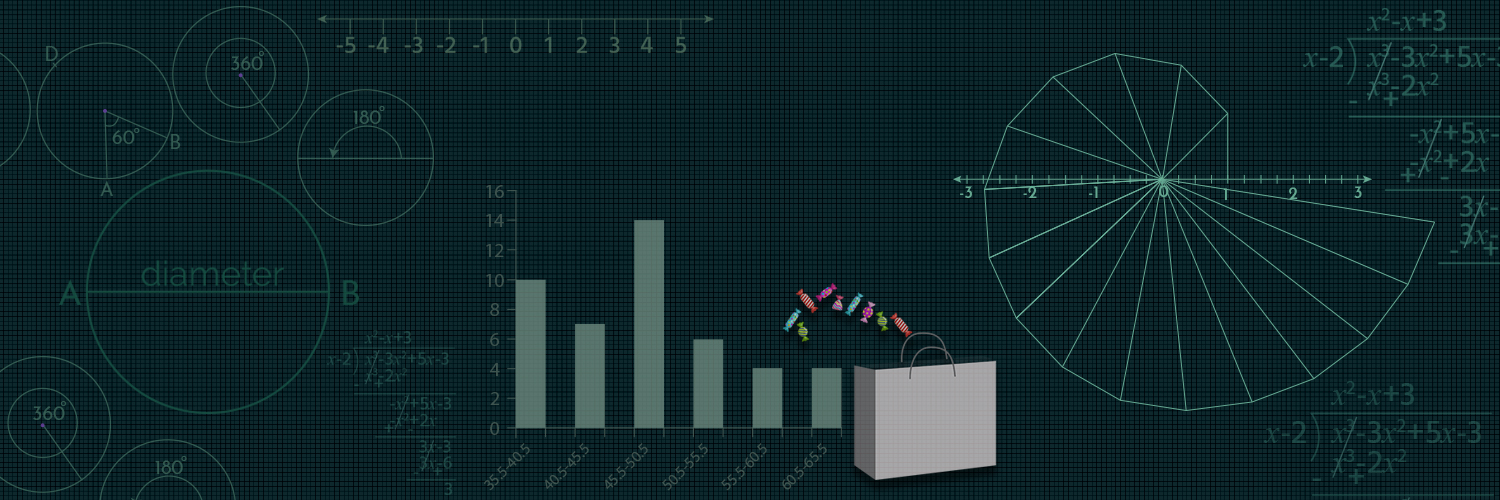
The line segment joining any two points of the circle is called chord.

Diameter(d) :

The diameter is chord passing through the centre.
It is the longest chord of the circle.
Diameter = 2 X r

Arc :

A piece of circle between any two points is called arc.

Central angle :

The angle formed at centre by joining end points of Chord /arc and centre is called centre angle of arc/chord.

Minor arc :

If central angle of an arc is acute ,the arc is called minor arc.

Major arc :

If central angle of an arc is obtuse, the arc is called major arc.

Semicircles :

The diameter divides part of circles in two equal arcs, called semicircles.

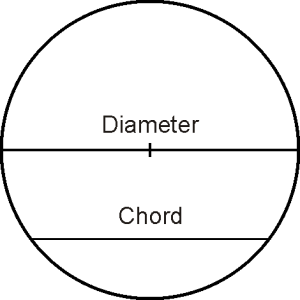
F o r s e m i c i r c l e a n g l e f o r m e d b y a r c s a t c e n t r e i s 180^{\circ} .

Segment :

The interior part of circle, the region between chord and arc is called segment.

Major segment :

The region between major arc and chord is called major segment.

Minor segment :

The region between minor arc and chord is called minor segment.

Sector :

The region between two radii and an arc is called sector.

Major Sector :

The region between two radii and an arc is called sector.

Minor Sector :

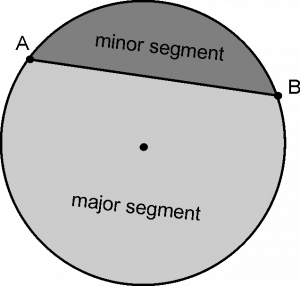
The region between minor arc and radii is called minor sector.

Theorem 1

Equal chords of a circle subtend equal angles at the centres.

Given :

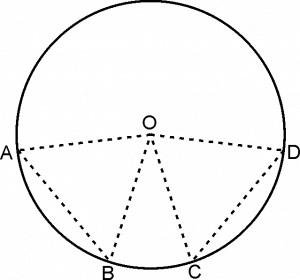
O is centre of the circle.
Chord AB = chord CD

To prove :

∠ A O B = ∠ C O D

Proof :

I n ∆ A O B a n d ∆ C O D

AB = CD …..(Given)

AO = CO …………….( Radii of same circle)

BO = DO ……………( Radii of same circle)

△ A O B ≅ △ C O D . . . . . . . . . . . . . . . . (S S S r u l e)

S o, ∠ A O B = ∠ C O D . . . . . . . . . . . . . . . . . (C P C T)

Theorem 2

If angles subtended by the chord of a circle at the centre are equal, then the Chords are equal.

Given :

O is centre of the circle.

∠ A O B = ∠ C O D

To prove :

∠ A O B = ∠ C O D

Proof :

I n ∆ A O B a n d ∆ C O D

∠ A O B = ∠ C O D . . . . . . . . . . . . . . (G i v e n)

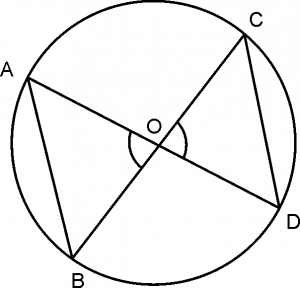
AO = CO …………….( Radii of same circle)

BO = DO ……………( Radii of same circle)

△ A O B ≅ △ C O D . . . . . . . . . . . . . . . . (S O S r u l e)

∴ A B = C D . . . . . . . . . . . . . . . . . (C P C T)

Theorem 3

Perpendicular from centre to a chord bisects the chord.

Given:

O is centre of the circle.

AB is chord.

O M ⊥ A B

To prove :

OM bisects AB i.e. AM = BM

Proof :

I n r i g h t ∆ A O M a n d ∆ B O M

AO = BO ……….(Radii)

OM = OM ………..(Common)

∠ A M O = ∠ B M O

∆ A O M = ∆ B O M \dots \dots . (R - H S r u l e)

So, AM = BM …………….. (CSCT)

Theorem 4

The line joining centre and midpoint of chord is perpendicular to chord.

Given:

O is centre of the circle.

AB is chord.

M is midpoint Of AB,

∴ A M = B M

To prove :

O M ⊥ A B

Proof:

I n ∆ A O M = ∆ B O M

AO = BO ………(Radii)

OM = OM……. (Common_

AM = BM………(Given)

∆ A O M = ∆ B O M \dots \dots \dots \dots (S S S r u l e)

S o ∠ A M O = ∠ B M O (C P C T)

But

∠ A M O + ∠ B M O = 180^{\circ} (L i n e a r p a i r)

2 ∠ A M O = 180^{\circ} ∠ A M O = 90^{0}

S o O M ⊥ A B

Theorem 5

There is one and only one circle passing through three non-collinear points.

Remark: There is a unique circle passing through vertices of the triangle.

Theorem 6

Equal chords are equidistant from centre.

Given:

AB and CD are two chords.

AB = CD

O M ⊥ A B, O N ⊥ C D

To Prove:

ON = OM

Proof:

N, M a r e m i d p o i n t s o f A B a n d C D \dots (P e r p e n d i c u l a r f r o m c e n t r e t o a c h o r d b i s e c t s t h e t h e c h o r d)

∴ A N = \frac{1}{2} A B

C M = \frac{1}{2} C D

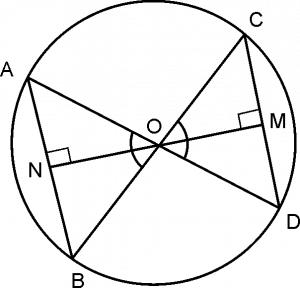
But, AB = CD

∴ A N = C M . . . (1)

I n r i g h t ∆ O C M a n d ∆ O A N

AN = CM …(From 1)

OA = OC …(Radii)

∆ O C M ≅ ∆ O A N . . . . . (R . H . S r u l e)

∴ O N = O M . . . . . (C P C T)

Theorem 7 : Converse:

Chords equidistant from centre are equal.

Given:

AB and CD are two chords.

O M ⊥ A B, O N ⊥ C D

ON = OM (As chords are equidiastantfrom the centre)

To prove:

AB = CD

Proof:

I n r i g h t ∆ O C M a n d ∆ O A N

ON = OM …(Given)

OA = OC …(Radii)

∆ O C M ≅ ∆ O A N . . . . \dots . . (R H S r u l e)

< Previous Chapter

Next Chapter >

Number System

Polynomials

Coordinate geometry

Linear equations in two variables

Introduction to Euclid’s geometry

Lines and angles

Triangles

Quadrilaterals

Areas of parallelogram

Constructions

Heron’s formula

Surface areas and volumes

Statistics

Probability

Start your learning Journey !

Get SMS link to download the app

Circles

10 Circles

CIRCLES

Circle :

Centre:

Radius(r):

Interior region of circle:

Exterior region of the circle:

Chord :

Diameter(d) :

Arc :

Central angle :

Minor arc :

Major arc :

Semicircles :

Segment :

Major segment :

Minor segment :

Sector :

Major Sector :

Minor Sector :

Theorem 1

Given :

To prove :

Proof :

Theorem 2

Given :

To prove :

Proof :

Theorem 3

To prove :

Proof :

Theorem 4

Given:

To prove :

Proof:

Theorem 5

Theorem 6

Given:

To Prove:

Proof:

Theorem 7 : Converse:

Given:

To prove:

Related Posts

Classes

Exams

About Us

Contact Us

Careers

Customer Stories