Triangles

Tutormate > CBSE Syllabus-Class 10th Maths > Triangles

06 TRIANGLES

Similarity:

Two figures are similar if their shapes are same but size may not be the same.

e.g Tajmahal and model of Tajmahal

Similarity of triangles:

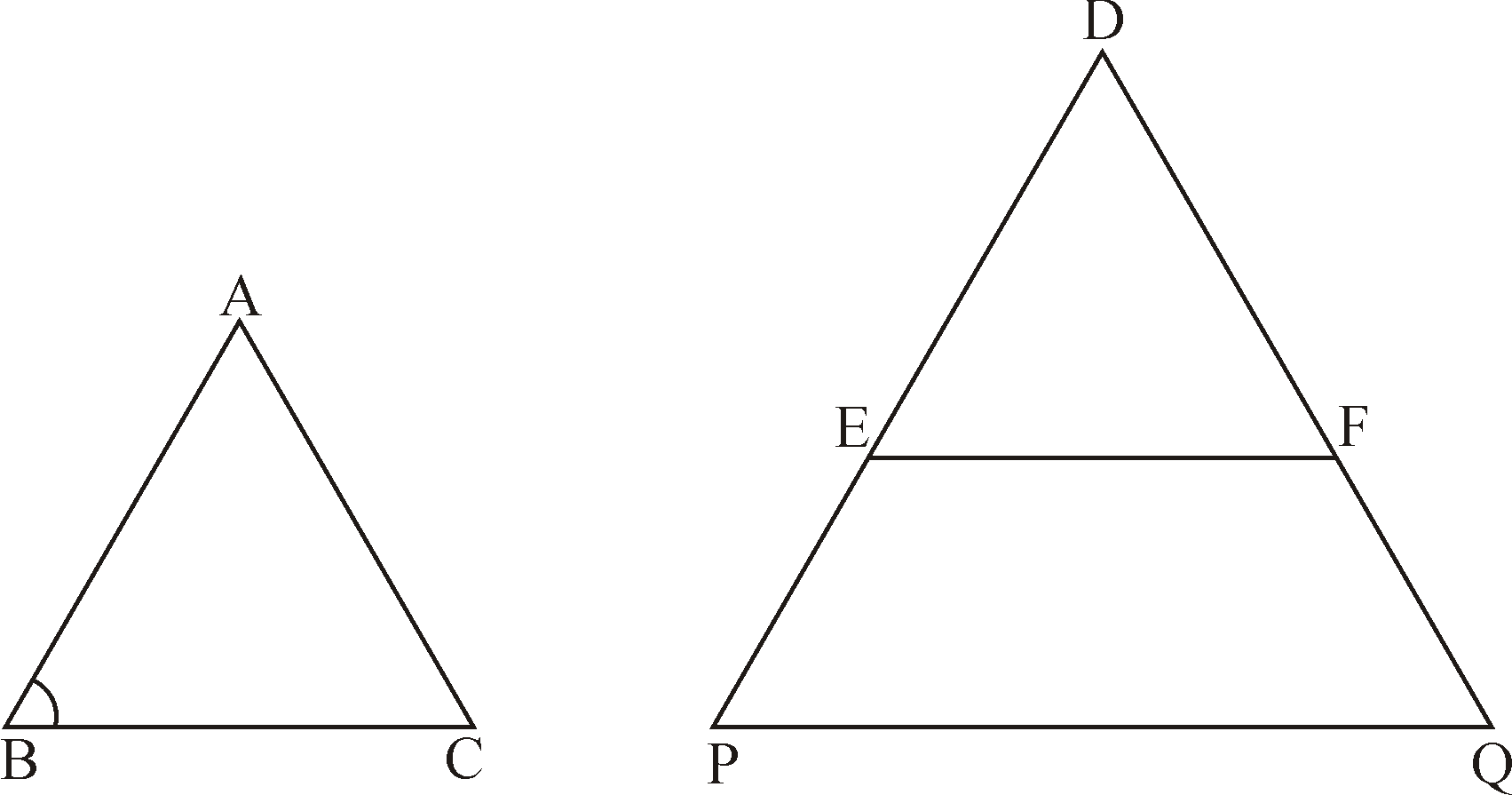
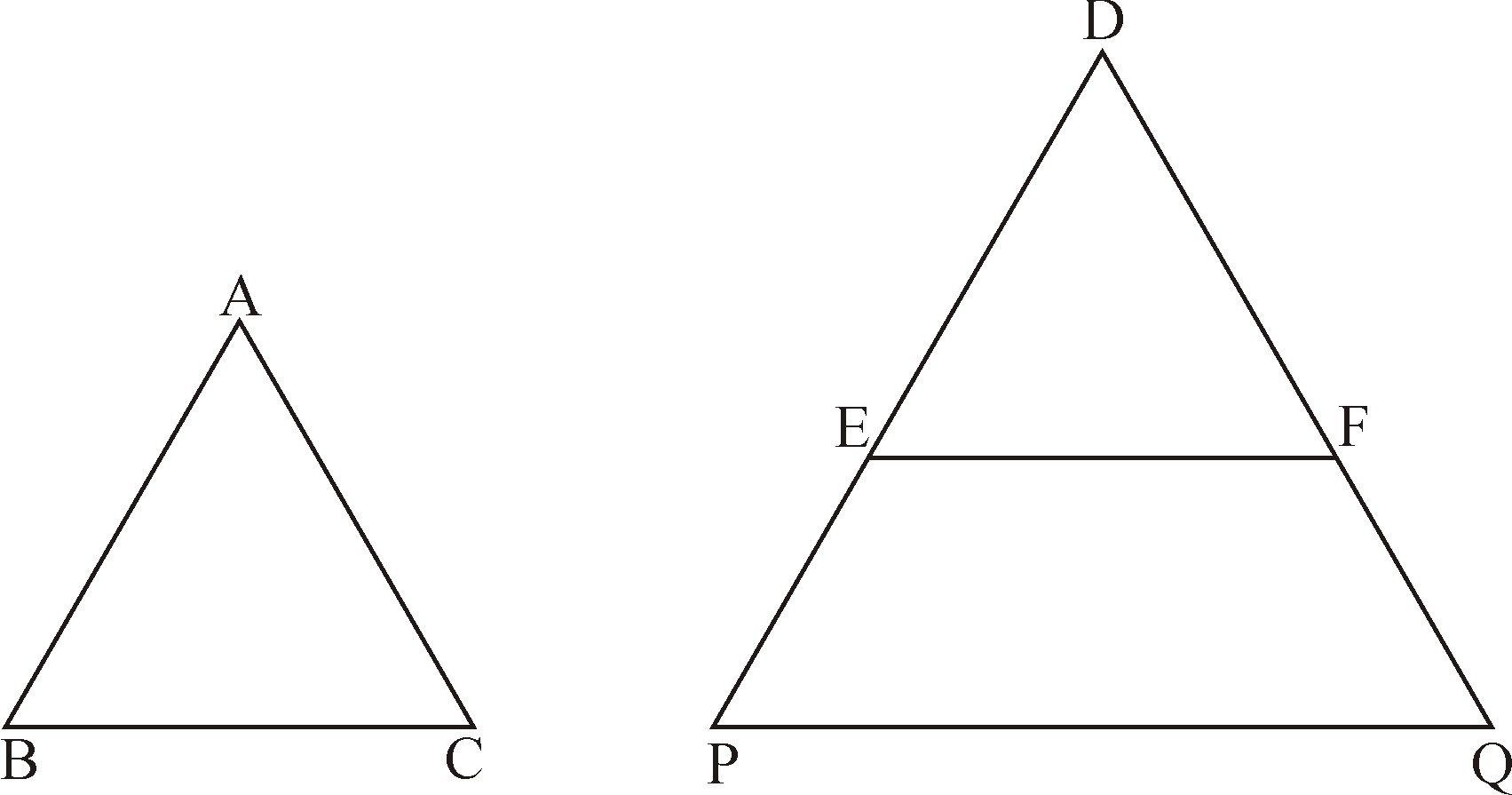
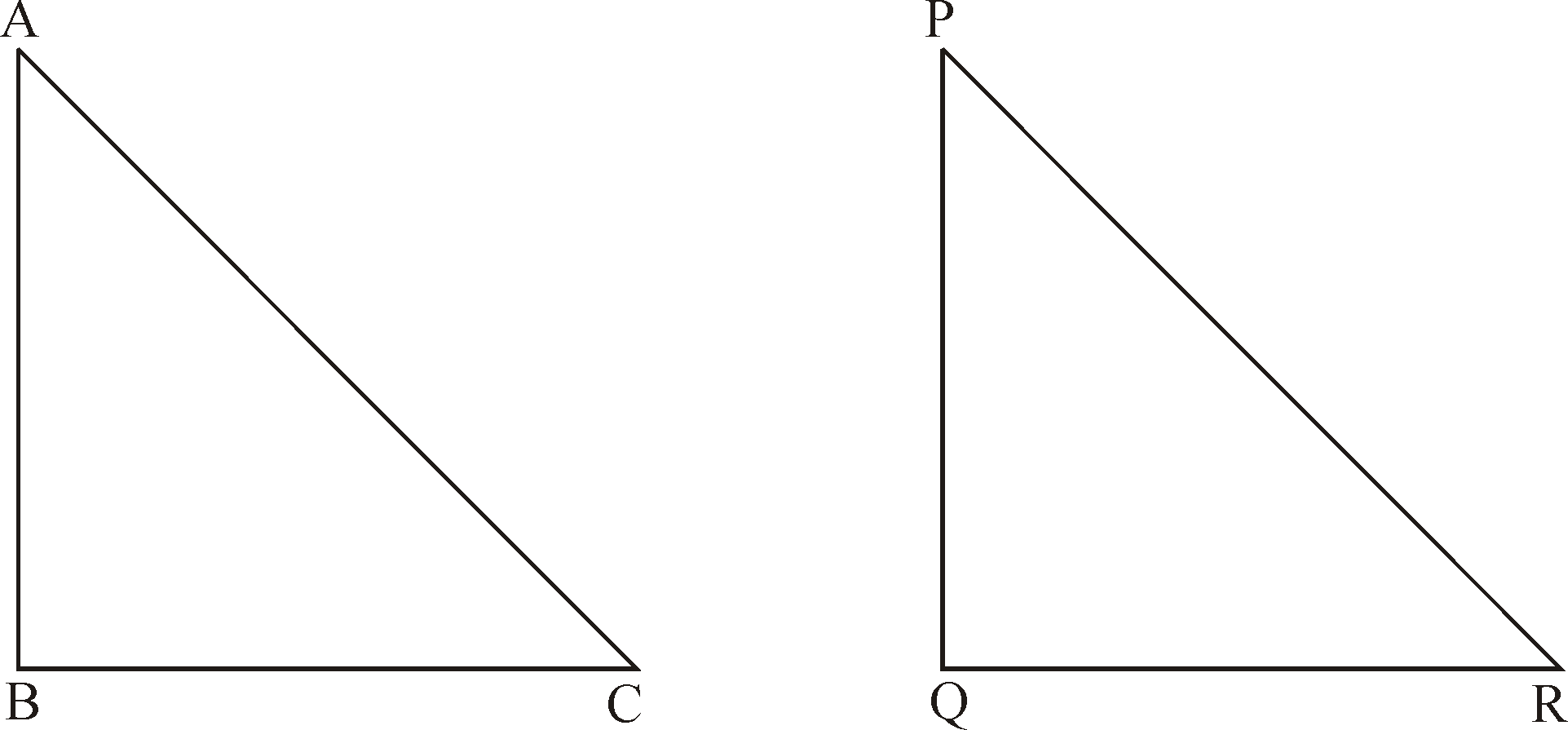
Two triangles Δ ABC and Δ PQR are similar

If 1) Their corresponding angles are equal i.e

∠ A = ∠ P, ∠ B = ∠ Q, ∠ C = ∠ R

2) Their corresponding sides are in proportion i.e.

\frac{A B}{P Q} = \frac{B C}{Q R} = \frac{A C}{P R}

A n d w e d e n o t e i t b y △ A B C ~ △ P Q R

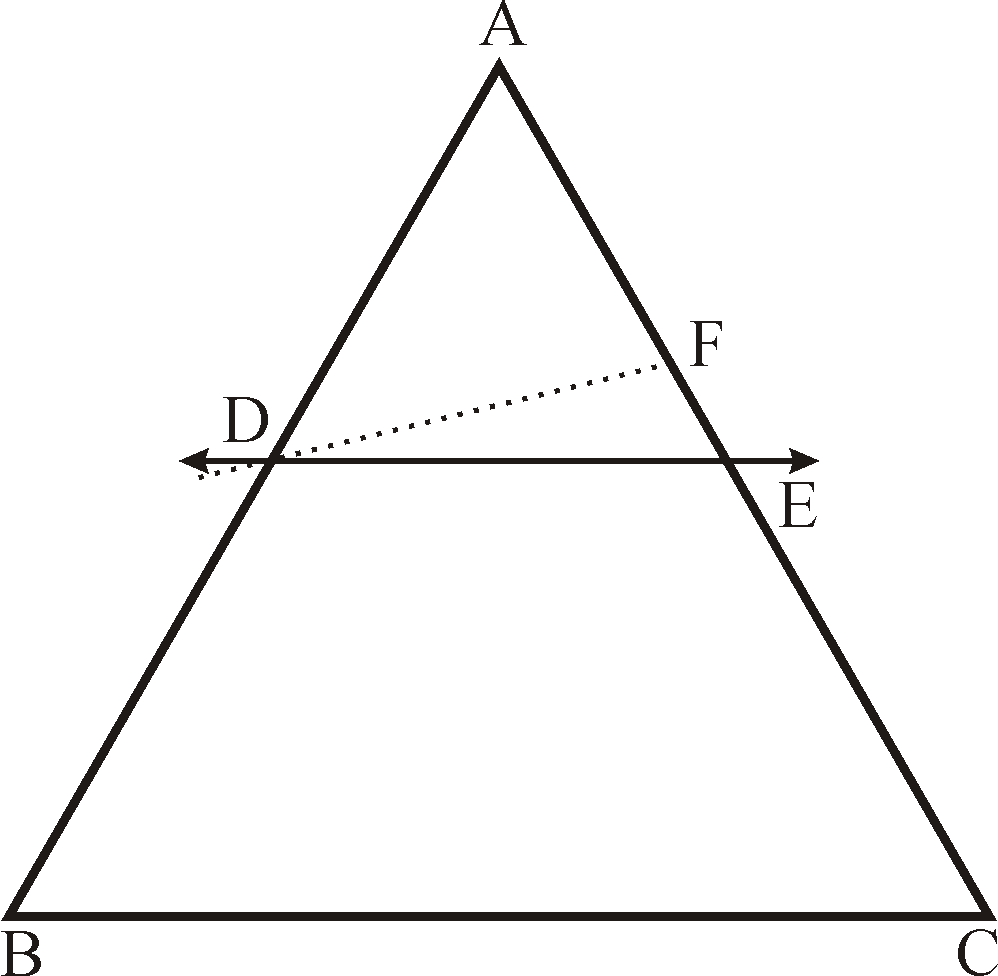
Theorem 1:Basic proportionality Theorem:(Thale’s Theorem)

If a line is drawn parallel to one side of triangle intersecting the other two sides, then

it divides the two sides in the same ratio.

Given: A triangle ABC in which

, and DE intersects AB at D and AC at E.

T O P R O V E : \frac{A D}{D B} = \frac{A E}{A C}

C O N S T R U C T I O N : J o i n B E, C D a n d d r a w E F ⊥ B A a n d D G ⊥ C A .

P r o o f : A r e a (△ A B E) = \frac{1}{2} (b a s e \times h e i g h t) = \frac{1}{2} (A D \times E F) : A r e a (△ D B E) = \frac{1}{2} (b a s e \times h e i g h t) = \frac{1}{2} (D B \times E F)

∴ \frac{A r e a (△ A D E)}{A r e a (△ D B E)} = \frac{\frac{1}{2} (A D \times E F)}{\frac{1}{2} (D B \times E F)} = \frac{A D}{D B} . . . . . . . (1) s i m i l a r l y, \frac{A r e a (△ A D E)}{A r e a (△ D E C)} = \frac{\frac{1}{2} (A E \times D G)}{\frac{1}{2} (E C \times D G)} = \frac{A E}{E C} . . . . . . . (2)

∴ A r e a (△ D B E) = A r e a (△ D E C) [t r i a n g l e s w i t h t h e s a m e b a s e D E a n d b e t w e e n t h e s a m e p a r a l l e l s D E a n d B C .]

\Rightarrow \frac{1}{A r e a (△ D B E)} = \frac{1}{A r e a (△ D E C)} [T a k i n g r e c i p r o c a l s]

\Rightarrow \frac{A r e a (△ A D E)}{A r e a (△ D B E)} = \frac{A r e a (△ A D E)}{A r e a (△ D E C)} [M u l t i p l y i n g b y A r e a]

\Rightarrow \frac{A D}{D B} = \frac{A E}{E C} [U \sin g (1) a n d (2)]

C O R O L L A R Y : I f i n a △ A B C, a l i n e D E B C, i n t e r s e c t s A B a t D a n d A C a t E, t h e n : (i) \frac{A B}{A D} = \frac{A C}{A E} (i i) \frac{A B}{D B} = \frac{A C}{E C}

P R O O F (i) \frac{A D}{D B} = \frac{A E}{E C} [F r o m t h e b a s i c p r o p o r t i o n a l i t y t h e o r e m]

\Rightarrow \frac{D B}{A D} = \frac{E C}{A E} [T a k i n g r e c i p r o c a l s]

\Rightarrow 1 + \frac{D B}{A D} = 1 + \frac{E C}{A E} [A d d i n g 1 o n b o t h s i d e s]

\frac{A D + D B}{A D} = \frac{A E + E C}{A E}

\Rightarrow \frac{A B}{A D} = \frac{A C}{A E}

(i i) \frac{A D}{D B} = \frac{A E}{E C} [F r o m t h e b a s i c p r o p o r t i o n a l i t y t h e o r e m]

\Rightarrow \frac{A D}{D B} = \frac{A E}{E C} [A d d i n g 1 o n b o t h s i d e s]

\Rightarrow \frac{A D + D B}{D B} = \frac{A E + E C}{E C}

\Rightarrow \frac{A B}{D B} = \frac{A E}{E C}

THEOREM 2:(Converse of Basic Proportionality Theorem)

If a line divides any two sides of a triangle in the same ratio, then the line must be

Parallel to the third side.

G I V E N : I n △ A B C, a l i n e D E i n t e r s e c t i n g A B a n d A C a t D, E, r e s p e c t i v e l y .

\frac{A D}{D B} = \frac{A E}{E C}

T O P R O V E : D E ∥ B C

P R O O F : I f p o s s i b l e, l e t D E b e n o t p a r a l l e l t o B C . T h e n, t h e r e m u s t b e a n o t h e r l i n e p a r a l l e l t o B C .

L e t D F ∥ B C

\frac{A D}{D B} = \frac{A F}{F C} (B Y B P T) . . . . . (i)

B u t \frac{A D}{D B} = \frac{A E}{E C} (G I i v e n) . . . . . . . \dots (i i)

From (i) and (ii), we get

\frac{A F}{F C} = \frac{A E}{E C}

\Rightarrow \frac{A F}{A C} + 1 = \frac{A E}{E C} + 1 [A d d i n g 1 o n b o t h s i d e s]

\Rightarrow \frac{A C}{F C} = \frac{A C}{E C}

\Rightarrow E C = E C

T h i s i s p o s s i b l e o n l y w h e n F a n d E c o i n c i d e B u t D F ∥ B C . H e n c e, D F ∥ B C .

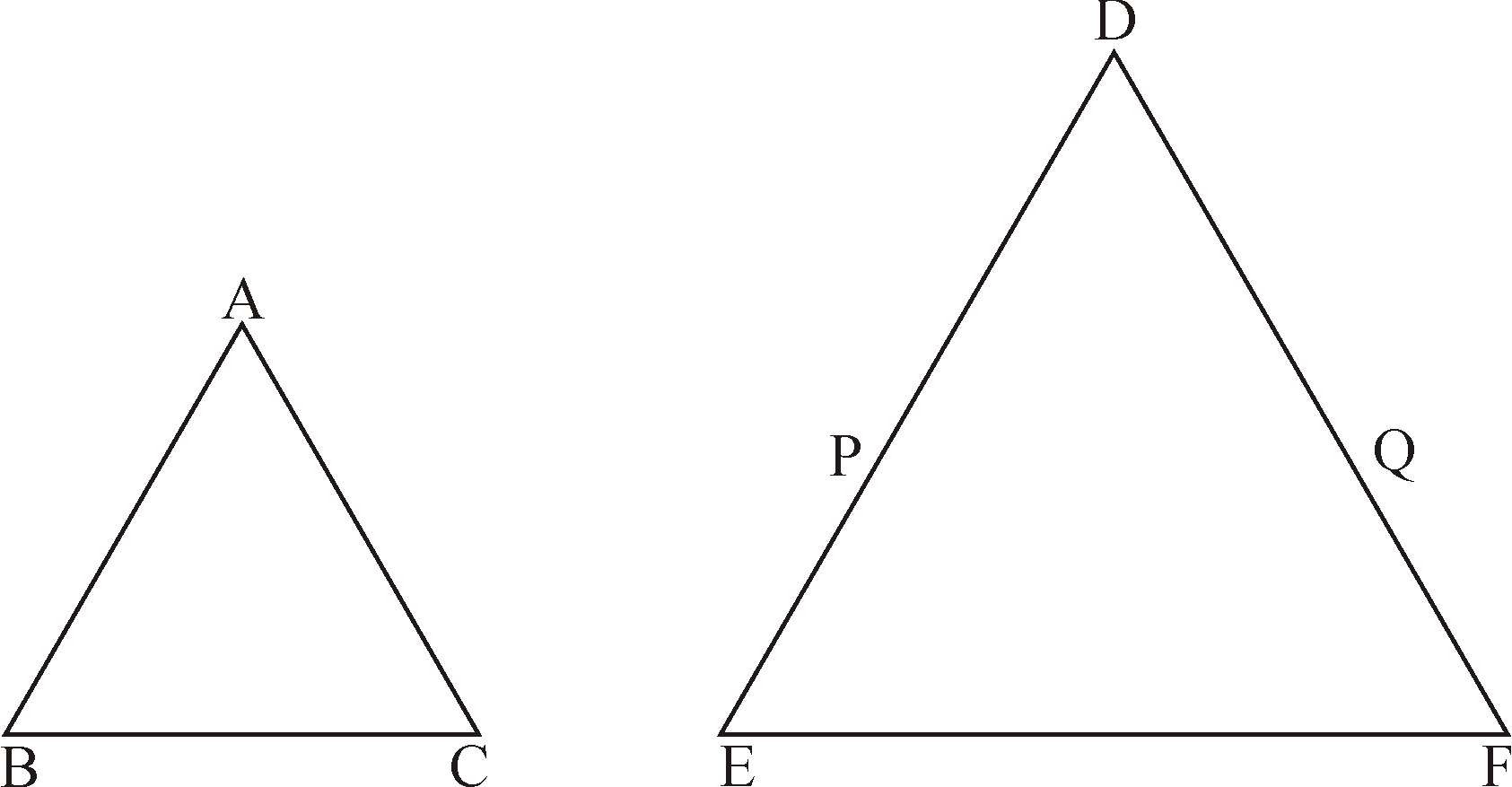
THEOREM 3(Angle bisector theorem):

The internal bisector of an angle of a triangle divides the opposite side internally in

the ratio of the sides containing the angle.

G I V E N : I n, A D i s b i s e c t o r o f ∠ A .

T O P R O V E : \frac{B D}{D C} = \frac{A B}{A C}

C O N S T R U C T I O N : D r a w C E ∥ D A . L e t C E m e e t B A p r o d u c e d i n E .

P R O O F : S i n c e C E ∥ D A a n d A C i s t r a n s v e r s a l .

∴ ∠ 2 = ∠ 3 \dots (i) [A l t e r n a t e a n g l e s]

a n d, ∠ 1 = ∠ 4 \dots (i i) [c o r r e s p o n d i n g a n g l e s]

B u t, ∠ 1 = ∠ 2 [∵ A D i s t h e b i s e c t o r o f ∠ A]

From (i) and (ii), we get

∠ 3 = ∠ 4

T h u s, i n △ A C E

\Rightarrow A E = A C \dots (i i i) [S i d e s o p p o s i t e t o e q u a l a n g l e s a r e e q u a l]

N o w, i n △ B C E, D A ∥ C E

\Rightarrow \frac{B D}{D C} = \frac{B A}{A E} [U \sin g B a s i c P r o p o r t i o n a l i t y T h e o r e m]

\Rightarrow \frac{B D}{D C} = \frac{A B}{A C} [A E = A C]

H e n c e, \frac{B D}{D C} = \frac{A B}{A C}

THEOREM 4(Converse of angle bisector theorem):

I n T r i a n g l e A B C, i f D i s a p o i n t o n B C s u c h t h a t, \frac{B D}{D C} = \frac{A B}{A C}

p r o v e t h a t A D i s t h e b i s e c t o r o f ∠ A .

G I V E N : I n A B C, i n w h i c h D i s a p o i n t o n B C s u c h t h a t \frac{B D}{D C} = \frac{A B}{A C}

T O P R O V E : A D i s t h e b i s e c t o r o f ∠ A .

CONSTRUCTION :Produce BA to E such that AE = AC. Join EC

P R O O F : I n △ A B C, w e h a v e A E = A C

\Rightarrow ∠ 3 = ∠ 4

Now,

\frac{B D}{D C} = \frac{A B}{A C}

T h u s, i n △ B C E, w e h a v e

\frac{B D}{D C} = \frac{A B}{A E} [∵ A C = A E]

D A ∥ C E (B y c o n v e r s e o f B P T)

\Rightarrow ∠ 1 = ∠ 4 \dots (i i) [C o r r e s p o n d i n g a n g l e s]

a n d, ∠ 2 = ∠ 3 \dots (i i i) [A l t e r n a t e a n g l e s]

B u t, ∠ 3 = ∠ 4 [F r o m (i)]

∴ ∠ 1 = ∠ 2 . . . . . . [F r o m (i i) a n d (i i i)]

H e n c e, A D i s t h e b i s e c t o r o f ∠ A .

THEOREM 5:

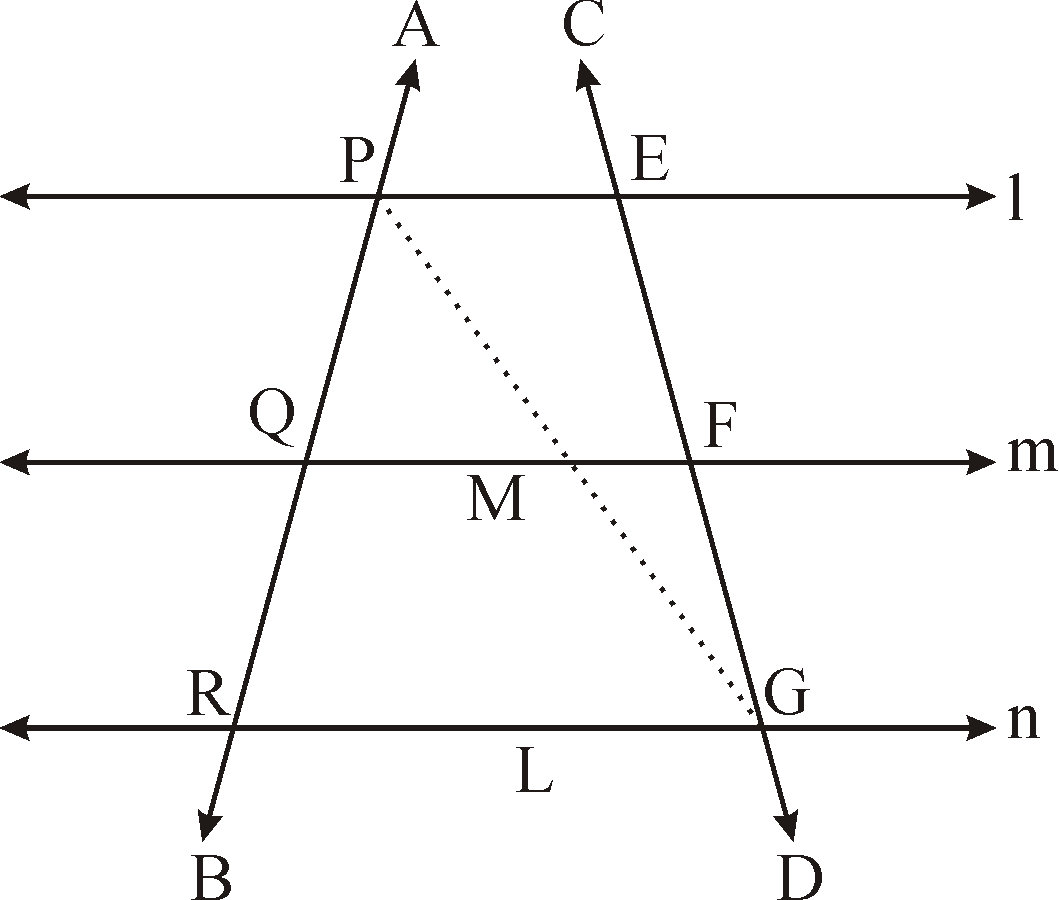
If three or more parallel lines are intersected by two transversals, prove that the

intercepts made by them on the transversals are proportional.

GIVEN:Three parallel lines l, m, n which are cut by the transversals AB and CD at P, Q, R and E, F, G respectively.

T O P R O V E : \frac{P Q}{Q R} = \frac{E F}{F G}

CONSTRUCTION: join PG.

PROOF:

I N △ P R G, Q M ∥ R G \Rightarrow \frac{P Q}{Q R} = \frac{P M}{M G} \dots (i) (B y T h a l e ’ s t h e o r e m)

N o w, i n △ P E G, w e h a v e

F M ∥ P E

\Rightarrow \frac{E F}{F G} = \frac{P M}{M G} . . (i i) (B y B P T)

H e n c e, \frac{P Q}{Q R} = \frac{E F}{F G} . . . . [U \sin g (i) a n d (i i)]

Criteria for similarities of triangles:

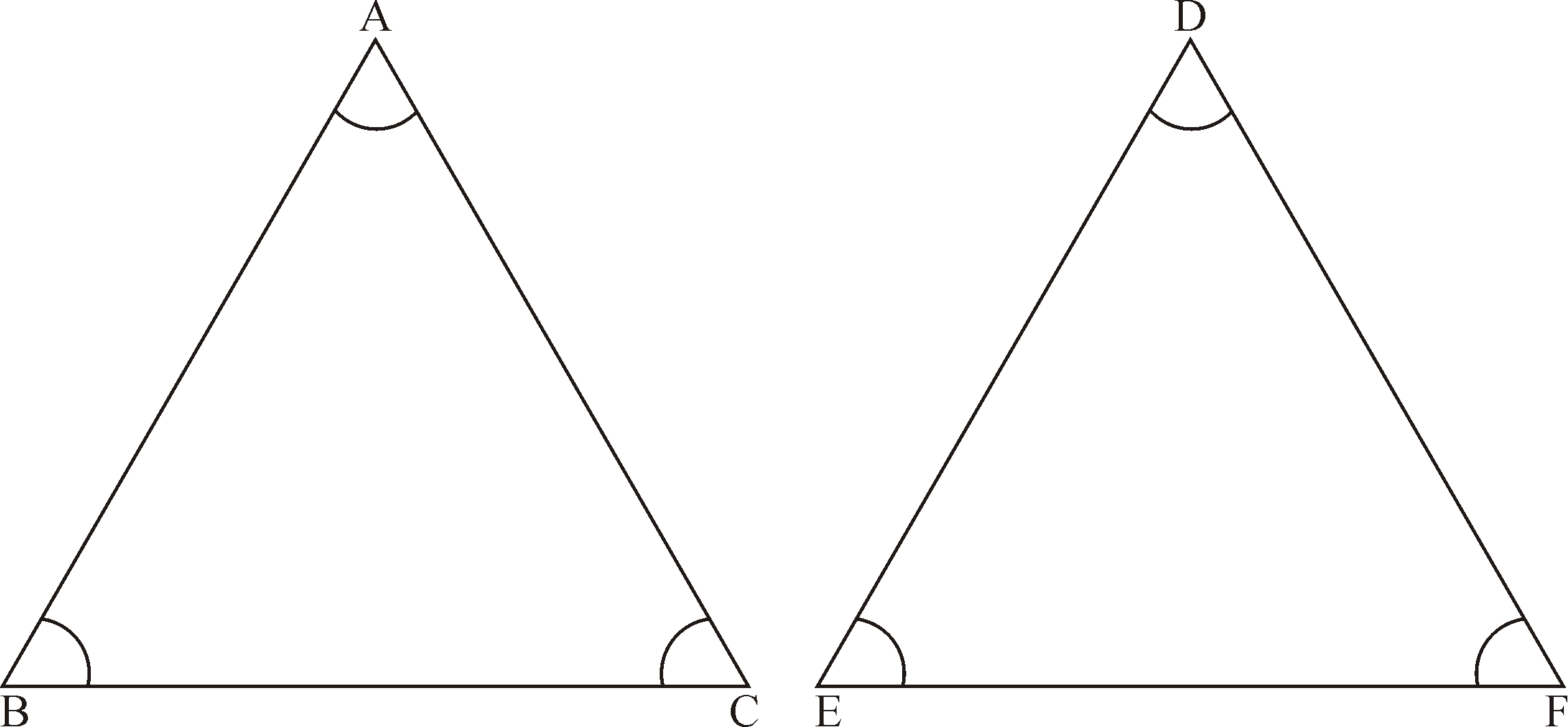
THEOREM6:(AAA Similarity Criterion):

If two triangles are equiangular, then they are similar.

G I V E N : T w o t r i a n g l e s A B C a n d D E F s u c h t h a t ∠ A = ∠ D, ∠ B = ∠ E a n d ∠ C = ∠ F

T O P R O V E : △ A B C ∥ △ D E F i . e \frac{A B}{D E} = \frac{B C}{E F} = \frac{A C}{D F}

PROOF: We can have AB=DE,,AB>DE,AB<DE

Case I: When AB = DE.

In this case, we have

∠ A = ∠ D, ∠ B = ∠ E, ∠ C = ∠ F a n d A B = D E

△ A B C ≅ △ D E F . . . (B y A S A c r i t e r i o n o f c o n g r u e n c y)

\Rightarrow A B = D E, B C = E F a n d A C = D F

\frac{A B}{D E} = \frac{B C}{E F} = \frac{A C}{D F}

Hence proved

C a s e I I : W h e n A B < D E .

Take a point P on the line DE and Q on the line DF such that AB = DP and AC = DQ.

Join PQ.

I n △ A B C a n d △ D P Q,

A B = D P, ∠ A = ∠ D, A C = D Q

∴ △ △ A B C ≅ △ D P Q [B y S A S c r i t e r i o n o f c o n g r u e n c e]

∠ B = ∠ D P Q

b u t ∠ B = ∠ E = ∠ D E F

∴ ∠ D P Q = ∠ D E F

\Rightarrow P Q ∥ E F [C o r r e s p o n d i n g a n g l e s a r e e q u a l]

\frac{D P}{D E} = \frac{D Q}{D F} [B y c o r o l l a r y o f T h a l e ’ s T h e o r e m]

Similarly, we can prove that

\frac{A B}{D E} = \frac{B C}{E F}

\frac{A B}{D E} = \frac{B C}{E F} = \frac{A C}{D F}

Hence proved

Case III:When AB > DE

Take a point P on the line DE produced and Q on the line DF produced

so that DP = AB and DQ = AC.

Join PQ.

I n △ A B C a n d △ D P Q, w e h a v e

A B = D P, A C = D Q, ∠ A = ∠ D

∴ A B C ≅ D P Q [B y S A S c r i t e r i o n o f c o n g r u e n c e]

∠ D = ∠ D P Q

b u t ∠ D = ∠ E = ∠ D E F

\Rightarrow P Q ∥ E F [C o r r e s p o n d i n g a n g l e s a r e e q u a l]

\frac{D E}{D P} = \frac{D F}{D Q} [B y c o r o l l a r y o f T h a l e ’ s T h e o r e m]

\frac{A B}{D E} = \frac{A C}{D F}

Similarly, we can prove that

\frac{A B}{D E} = \frac{B C}{E F}

\frac{A B}{D E} = \frac{B C}{E F} = \frac{A C}{D F}

hence proved

THEOREM 7: (SSS Similarity Criterion)

If the corresponding sides of two triangles are proportional, then they are similar.

G I V E N : T w o t r i a n g l e s A B C a n d D E F s u c h t h a t \frac{A B}{D E} = \frac{B C}{E F} = \frac{A C}{D F}

T O P R O V E : △ A B C ∥ △ D E F

CONSTRUCTION:Let P and Q be points on DE and DF respectively

such that DP = AB and DQ = AC.

Join PQ.

PROOF :We have,

\frac{A B}{D E} = \frac{A C}{E F}

\frac{D P}{D E} = \frac{D Q}{D F} [A B = D P a n d A C = D Q]

\Rightarrow P Q ∥ E F [B y t h e c o n v e r s e o f T h a l e ’ s T h e o r e m]

∠ D P Q = ∠ E a n d ∠ D P Q = ∠ F [C o r r e s p o n d i n g a n g l e s]

Thus, in triangles DPQ and DEF, we have

∠ D P Q = ∠ E a n d ∠ D P Q = ∠ F

△ D P Q ∥ ∆ D E F (A - A c r i t e r i a o f s i m i l a r i t y)

\frac{D P}{D E} = \frac{P Q}{E F} [B y d e f . o f s i m i l a r i t y]

\frac{A B}{D E} = \frac{P Q}{E F} [∵ D P = A B]

\Rightarrow P Q = B C

S o i n △ A B C a n d △ D P Q,

A B = D P, A C = D Q a n d B C = P Q

A B = D P, A C = D Q a n d B C = P Q

△ A B C ≅ △ D P Q (b y S S S c r i t e r i o n o f c o n g r u e n c e)

From (i) and (ii), we have

△ A B C ≅ △ D P Q a n d △ D P Q ∥ △ D E F

\Rightarrow △ A B C ∥ △ D E F

THEOREM 8(SAS similarity Criterion):

If in two triangles, one pair of corresponding sides are proportional and the

included angles are equal then the two triangles are similar.

G I V E N : I n △ A B C a n d △ D E F, ∠ A = ∠ D a n d \frac{A B}{D E} = \frac{A C}{D F}

T O P R O V E : △ A B C ∥ △ D E F

CONSTRUCTION: Take points P and Q on DE and DF respectively,so that

DP = AB and DQ = AC. Join PQ.

P R O O F : I n △ A B C a n d △ D P Q, w e h a v e

A B = D P, ∠ A = ∠ D a n d A C = D Q

△ A B C ≅ △ D P Q (i) . . . . . (b y S A S C r i t e r i o n o f C o n g r u e n c e)

N o w, \frac{A B}{D E} = \frac{A C}{D F}

\Rightarrow \frac{D P}{D E} = \frac{D Q}{D F} [A B = D P a n d A C = D Q]

\Rightarrow P Q ∥ E F [B y t h e c o n v e r s e o f B P T]

∠ D P Q = ∠ E a n d ∠ D Q P = ∠ F . . . . . [C o r r e s p o n d i n g a n g l e s]

D P Q ∥ D F Q

…(ii), (by AAA-criterion of similarity)

From (i) and (ii), we get

△ A B C ≅ △ D P Q a n d △ D P Q ≅ △ D E F

\Rightarrow △ A B C ∥ △ D E F

Areas of similar triangles:

Theorem 9:

The ratio of areas of two similar triangles is equal to the square of the ratio of their

Corresponding sides

Given: Triangle ABC is similar to triangle PQR.

∠ A = ∠ P

∠ B = ∠ Q

∠ C = ∠ R

\frac{A B}{P Q} = \frac{A C}{P R} = \frac{B C}{Q R}

T o p r o v e : \frac{A (△ A B C)}{A (△ P Q R)} = {(\frac{A B}{P Q})}^{2} = {(\frac{A C}{P R})}^{2} = {(\frac{B C}{P Q^{}})}^{2}

C o n s t r u c t i o n : D r a w A M ⊥ B C a n d P N ⊥ Q R .

Proof:

A r e a o f t r i a n g l e s = \frac{1}{2} b a s e \times h e i g h t

A (△ A B C) = \frac{1}{2} B C \times A M

A (△ P Q R) = \frac{1}{2} Q R \times P N

\frac{A (△ A B C)}{A (△ P Q R)} = \frac{\frac{1}{2} \times B C \times A M}{\frac{1}{2} \times Q R \times P N} = \frac{B C \times A M}{Q R \times P N}

…. (i)

I n △ A B M a n d △ P Q N

∠ B = ∠ Q . . . . . . (G I V E N)

A n d ∠ M = ∠ N (a s b o t h 90, b y c o n s t r u c t i o n)

∴ △ A B M ∥ △ P Q N (b y A A t e s t) (f r o m s t a t e m e n t s A a n d B)

\frac{A B}{P Q} = \frac{B C}{Q R} = \frac{A M}{P N} \dots . (i i)

\frac{A (△ A B C)}{A (△ P Q R)} = \frac{B C \times A M}{Q R \times P N} = \frac{B C \times B C}{Q R \times Q R} = {(\frac{B C}{Q R})}^{2}

Similarly we can show for other side too.

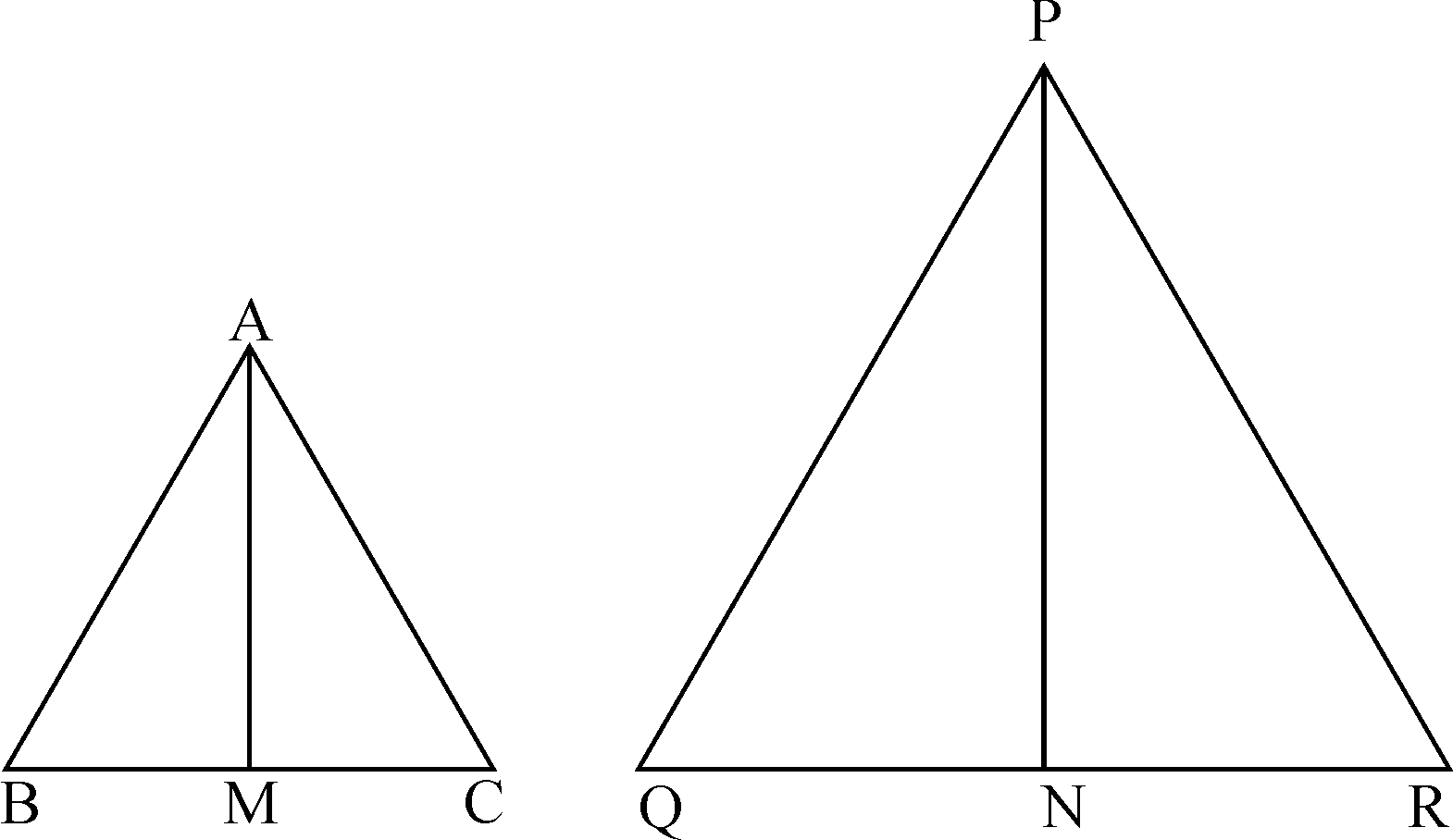
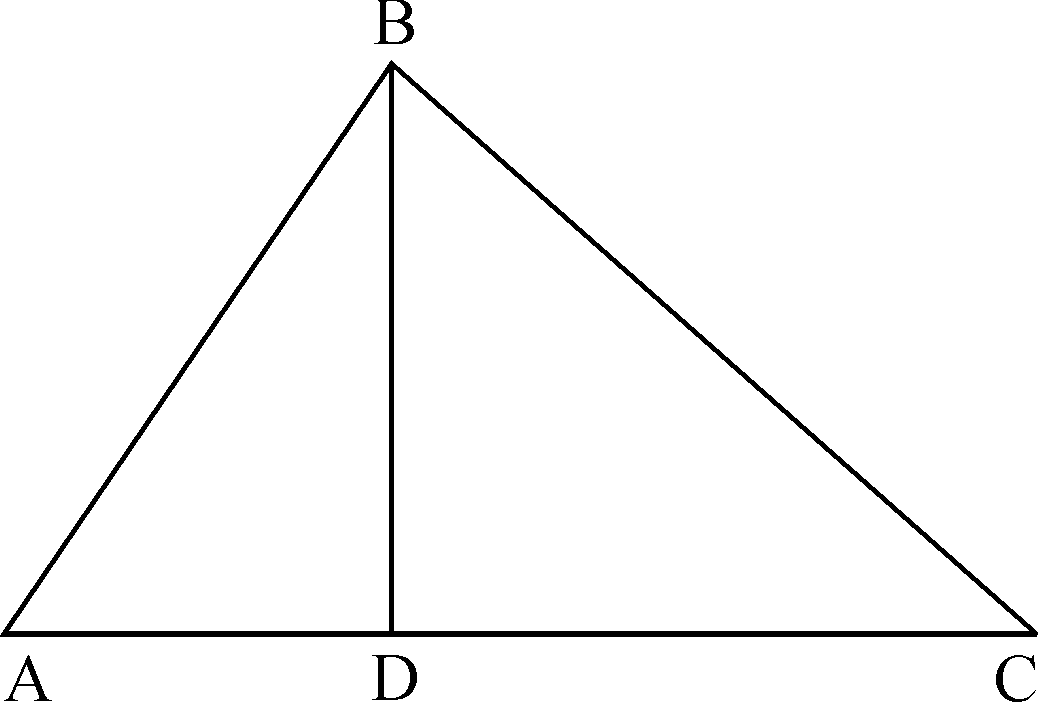
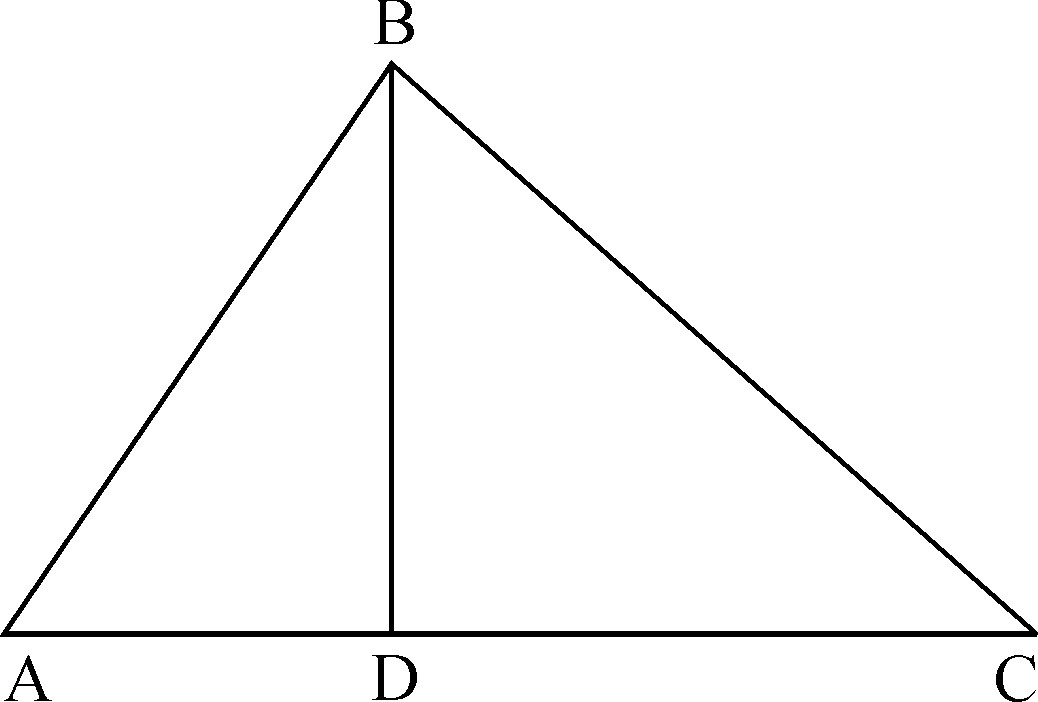
\frac{A (△ A B C)}{A (△ P Q R)} = {(\frac{A B}{P Q})}^{2} = {(\frac{B C}{Q R})}^{2} = (\frac{A C}{P R}) 2

Theorem 10:Theorem of three right angles triangles

If a perpendicular is drawn from the vertex of the right angle of a right angle

triangle to the hypotenuse then triangles on both sides of perpendicular are

similar to the whole triangle and each other.

G i v e n : B D ⊥ A C, i n △ A B C ∠ B = 90

T o p r o v e : △ A B C ∥ △ A D B ∥ △ B D C

Proof:

C o n s i d e r ∆ A B C, △ A D B

∠ A = ∠ A . . . . . . . . . (S a m e a n g l e)

∠ A D B = ∠ A B C . . . . . \dots . (b o t h 90)

△ A B C ∥ △ A D B \dots . (1) (b y A A c r i t e r i a)

i n ∆ A B C, △ B D C

∠ C = ∠ C (S a m e a n g l e)

∠ B D C = ∠ A B C . . . (b o t h 90)

△ A B C ∥ △ A D C \dots (2) (b y A A c r i t e r i a)

H e n c e △ A B C ∥ △ A D B ∥ △ B D C . . . . (F r o m 1 a n d 2)

Theorem 11: Pythagoras theorem:

In a right angle triangle,the square of the hypotenuse is equal to the sum of

squares of other two sides.

G i v e n : △ A B C, ∠ B = 90 °

T o p r o v e : A C^{2} = A B^{2} + B C^{2}

C o n s t r u c t i o n : D r a w B D ⊥ A C

P r o o f : A s B D ⊥ A C

△ A B C ∥ △ A D B ∥ △ B D C . . . . (B y t h e o r e m o f 3 r i g h t t r i a n g l e s)

C o n s i d e r △ A B C, △ A D B

C o n s i d e r △ A B C, △ A D B

\frac{A B}{A D} = \frac{B C}{B D} = \frac{A C}{A B}

\Rightarrow \frac{A B}{A D} = \frac{A C}{A B}

A B^{2} = A D \times A C . . . . (1)

N o w c o n s i d e r △ A B C ∥ △ B D C

\frac{A B}{B D} = \frac{B C}{D C} = \frac{A C}{B C}

\Rightarrow \frac{B C}{D C} = \frac{A C}{B C}

B C^{2} = C D \times A D . . . . . . (2)

= A C^{2}

A B^{2} + B C^{2} = C D \times A C + A D \times A C

= A C (C D + A D) . . . .) \dots \dots (T a k i n g A C c o m m o n)

Hence proved.

Theorem 12: Converse of Pythagoras theorem:

In a triangle, if square of one side is equal to the sum of squares of other two
sides, then the angle opposite the first side is a right angle.

G i v e n : A ∆ A B C, A C^{2} = A B^{2} + B C^{2}

T o P r o v e : ∠ B = 90^{\circ}

C o n s t r u c t i o n : C o n s t r u c t ∆ P Q R, P Q = A B, Q R = B C a n d ∠ Q = 90^{\circ}

Proof: In PQR we can apply Pythagoras theorem

S o, P R^{2} = P Q^{2} + Q R^{2}

O r, P R^{2} = A B^{2} + B C^{2} . . . . . . . . . . . . . . . . . . . . (1) (a s b y c o n s t r u c t i o n, P Q = A B, Q R = B C)

B u t A C^{2} = A B^{2} + B C^{2} . . . . . . . . . . . . . . . . . . . . . . . (2) (G i v e n)

So AC = PR (from 1 and 2)

N o w i n ∆ A B C a n d ∆ P Q R

AC = PR

PQ = AB,

QR = BC

∴ ∆ A B C = ∆ P Q R (b y S S S t e s t)

∴ ∠ Q = ∠ B

S o, ∠ B = 90^{\circ}

Proved..

< Previous Chapter

Next Chapter >

Real Numbers

Polynomials

Pair of linear equation

Quadratic Equation

Arithmetic Progression

Coordinate geometry

Introduction to trigonometry

Application of trigonometric ratio

Circles

Constructions

Areas related to circle

Surface areas and volumes

Statistics

Probability

Start your learning Journey !

Get SMS link to download the app

Triangles

06 TRIANGLES

< Previous Chapter

Next Chapter >

Related Posts

Real Numbers

Polynomials

Pair of linear equation

Quadratic Equation

Arithmetic Progression

Coordinate geometry

Introduction to trigonometry

Application of trigonometric ratio

Circles

Constructions

Areas related to circle

Surface areas and volumes

Statistics

Probability

Classes

Exams

About Us

Contact Us

Careers

Customer Stories