Introduction to trigonometry

Tigonometric Ratios :

In right angled triangle $\text{ABC}$

$\text{Sin θ = }\frac{\text{Opposite Sides to θ}}{\text{Hypotanuse}}$

$\text{Cos θ = }\frac{\text{Adjacent Sides to θ}}{\text{Hypotanuse}}$

$\text{Tan θ = }\frac{\text{Opposite Sides to θ}}{\text{Adjacent side to θ}}$

$\text{Cosec θ = }\frac{\text{Hypotanuse}}{\text{Opposite side to θ}}$

$\text{Sec θ = }\frac{\text{Hypotanuse}}{\text{Adjacent side to θ}}$

$\text{Cot θ = }\frac{\text{Adjacent Side to θ}}{\text{Opposite side to θ}}$

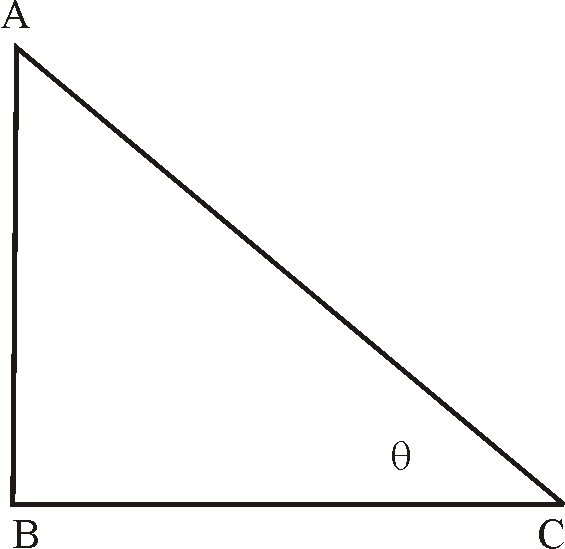
Relation between ratios:

$\text{Cosec θ = }\frac{\text{1}}{\text{Sin θ}}$

$\text{Sec θ = }\frac{\text{1}}{\text{Cos θ}}$

$\text{Cot θ = }\frac{\text{1}}{\text{Tan θ}}$

$\text{Tan θ = }\frac{\text{Sin θ}}{\text{Cos θ}}$

$\text{Cot θ = }\frac{\text{Cos θ}}{\text{Sin θ}}$

Trigonometric ratios of Specific angles:

Trigonometric Ratios of Complimentary Angles:

$\text{Sin}\left(\text{90°- θ}\right)\text{ = Cos θ}$

$\text{Cos}\left(\text{90°- θ}\right)\text{ = Sin θ}$

$\text{Tan}\left(\text{90°- θ}\right)\text{ = Cot θ}$

$\text{Sec}\left(\text{90°- θ}\right)\text{ = Cosec θ}$

$\text{Cosec}\left(\text{90°- θ}\right)\text{ = Sec θ}$

$\text{Cot}\left(\text{90°- θ}\right)\text{ = Tan θ}$

Trigonometric Identities:

${\text{Sin}}^{\text{2}}{\text{θ + cos}}^{\text{2}}\text{θ = 1}$

$1+{\tan }^2\theta ={\sec }^2\theta$

$1+{\cot }^2\theta ={\csc }^2\theta$

Proofs: In a $\Delta \text{ABC}$,

$\text{sin θ = }\frac{\text{AB}}{\text{AC}}\text{, cos θ = }\frac{\text{BC}}{\text{AC}}\text{, tan θ = }\frac{\text{AB}}{\text{BC}}\text{,}$

$\text{Cosec θ = }\frac{\text{AC}}{\text{AB}}\text{, sec θ = }\frac{\text{AC}}{\text{BC}}\text{, cot θ = }\frac{\text{BC}}{\text{AB}}\text{,}$

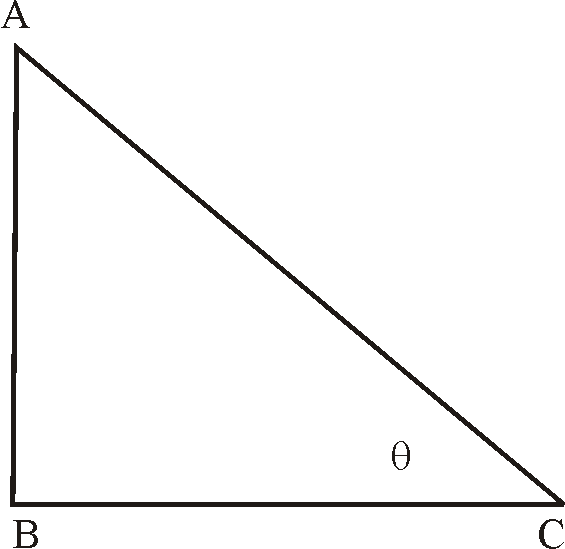
1) By Pythagoras theorem

${\text{AB}}^{\text{2}}{\text{ + BC}}^{\text{2}}{\text{ = AC}}^{\text{2}}$

Dividing by $A{C}^2$, we get

$\frac{{\text{AB}}^{\text{2}}}{{\text{AC}}^{\text{2}}}\text{ + }\frac{{\text{BC}}^{\text{2}}}{{\text{AC}}^{\text{2}}}\text{ = }\frac{{\text{AC}}^{\text{2}}}{{\text{AC}}^{\text{2}}}$

$\therefore {\text{Sin}}^{\text{2}}{\text{θ + cos}}^{\text{2}}\text{θ = 1}$

2) By Pythagoras theorem

${\text{AB}}^{\text{2}}{\text{ + BC}}^{\text{2}}{\text{ = AC}}^{\text{2}}$

Dividing by ${\text{BC}}^{\text{2}}$, we get

$\frac{{\text{AB}}^{\text{2}}}{{\text{BC}}^{\text{2}}}\text{ + }{\frac{\text{BC}}{{\text{BC}}^{\text{2}}}}^{\text{2}}\text{ = }\frac{{\text{AC}}^{\text{2}}}{{\text{BC}}^{\text{2}}}$

$\therefore {\text{tan}}^{\text{2}}{\text{θ + 1 = sec}}^{\text{2}}\text{θ}$

3) By Pythagoras theorem

${\text{AB}}^{\text{2}}{\text{ + BC}}^{\text{2}}{\text{ = AC}}^{\text{2}}$

Dividing by ${\text{AB}}^{\text{2}}$, we get

$\frac{{\text{AB}}^{\text{2}}}{{\text{AB}}^{\text{2}}}\text{ + }\frac{{\text{BC}}^{\text{2}}}{{\text{AB}}^{\text{2}}}\text{ = }\frac{{\text{AC}}^{\text{2}}}{{\text{AB}}^{\text{2}}}$

$\therefore {\text{1 + cot}}^{\text{2}}{\text{θ = cosec}}^{\text{2}}\text{θ}\text{.}$

Different forms of identities:

1) ${\text{Sin}}^{\text{2}}{\text{θ + cos}}^{\text{2}}\text{θ = 1}$ or ${\text{Cos}}^{\text{2}}{\text{θ = 1 - Sin}}^{\text{2}}\text{θ}$ or ${\text{Sin}}^{\text{2}}{\text{θ = 1 - Cos}}^{\text{2}}\text{θ}$

2) $1+{\tan }^2\theta ={\sec }^2\theta$ or ${\sec }^2\theta -{\tan }^2\theta =1$ or ${\tan }^2\theta ={\sec }^2\theta -1$

3) $1+{\cot }^2\theta =co{\sec }^2\theta$ or $co{\sec }^2\theta -{\cot }^2\theta =1$ or ${\cot }^2\theta =co{\sec }^2\theta -1$

.