linear equation in 2 variables

Tutormate > CBSE Syllabus-Class 10th Maths > linear equation in 2 variables

03 LINEAR EQUATION IN 2 VARIABLES:

Linear equation in two variables: It is the equation with two variables and with highest

power of variable or Degree .

General form:

a x^{2} + b x + c = 0 a n d b \neq 0

e . g . 2 x + 3 y = 4, 2 a + 3 b = 9

Solution of Linear equation in two variables: The values of and which satisfy the given

equation is called solution of the equation in two variables.

e.g. 2x +3y+4=0 has solution x=1 and y =-2.

X= -5 , Y= 2 is also solution of the equation.

The linear equation can have infinite solutions.
The graph of linear equation is a straight line.
The solution of a linear equation in variables is a point on the line graph.
Any point on line is the solution of linear equation representing line.

Pair of linear equations in 2 variables:

It contains two linear equations in same two variables

I n g e n e r a l i t i s w r i t t e n a s a_{1} x + b_{1} y + c_{1} = 0, a_{2} x + b_{2} y + c_{2} = 0

w i t h a_{1,} b_{1,} a_{2}, b_{2} a r e r e a l a n d {a_{1}}^{2} + {b_{1}}^{2} \neq 0

Geometric meaning of Pair of linear equations in variables:

G i v e n p a i r o f e q u a t i o n s : a_{1} x + b_{1} y + c_{1} = 0

a_{2} x + b_{2} y + c_{2} = 0

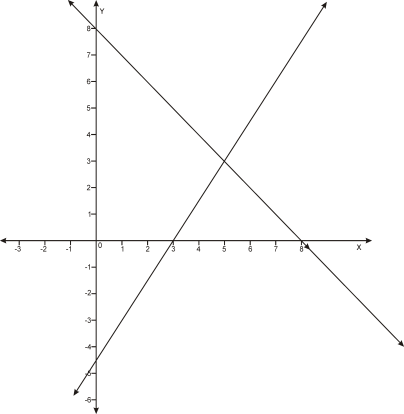
Case 1:

When two lines intersect at a single point.

There is unique solution.
Equations are called consistent.

° \frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b 2_{}}

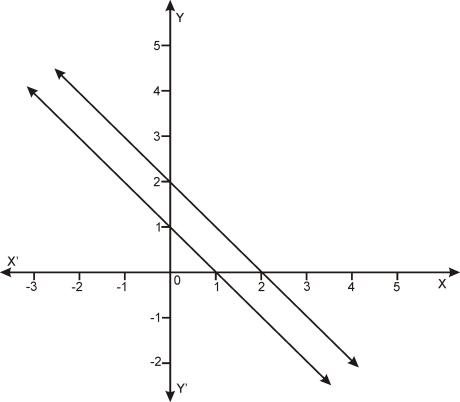
Case 2:

When two lines coincide with each other

There are infinitely many solution
Equations are called consistent

\frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} = \frac{c_{1}}{c_{2}}

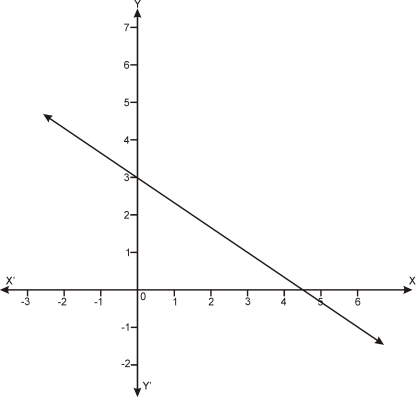
Case 3:

When two lines are parallel.

No solution exist
Equations are called inconsistent

\frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}

Algebraic method to solve pair of linear equations in variables:

Substitution method:

Find value of in terms of using any equation:
$e . g . y = \frac{c_{1} - a_{1} x}{b_{1}}$

Substitute this
$2^{n d}$
equation i.e. in
$a_{2} x + b_{2} y + c_{2} = 0$

Find the value of x(or y)
Put value x(or y) in eq in step 1.

Elimination Method:

Make coefficients of x (or y) equal by multiplying with suitable non zero real number.
Add or subtract both equations.
Get the value of y( or x).
Substitute value of y ( or x) in suitable equation and get value of other variable.

Cross multiplication method:

Arrange the coefficients as shown:

And we can write

\frac{x}{b_{1} c_{2} - b_{2} c_{1}} = \frac{y}{c_{1} a - c_{2} a_{1}} = \frac{1}{a_{1} b_{2} - a_{2} b_{1}}

Equations reducible to a pair linear equation in two variables:

T h e e q u a t i o n s \frac{a_{1}}{x} + \frac{b_{1}}{y} = c_{1}, \frac{a_{2}}{x} + \frac{b_{2}}{y} = c_{2}

S u b s t i t u t e \frac{1}{x} = p, \frac{1}{y} = q

A n d e q . s r e d u c e t o a_{1} p + b_{1} q + c_{1} = 0 a_{2} p + b_{2} q + c_{2} = 0

This is pair of linear equations in variables and .

< Previous Chapter

Next Chapter >

Real Numbers

Polynomials

Quadratic Equation

Arithmetic Progression

Triangles

Coordinate geometry

Introduction to trigonometry

Application of trigonometric ratio

Circles

Constructions

Areas related to circle

Surface areas and volumes

Statistics

Probability

Start your learning Journey !

Get SMS link to download the app