Circles

Tangent to the circle: 

A line that intersects the circle at only one point is called a tangent.

* There is only one tangent at a point on the circle.

* There are two tangents to a circle from a point outside the circle.

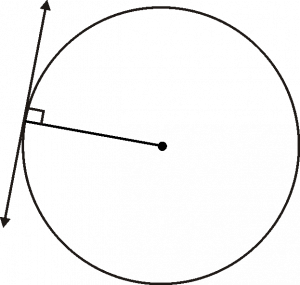
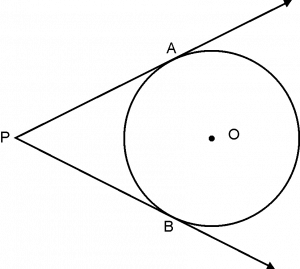
Length of tangent : 

The length of tangent from the external point and point of contact with the circle is called the length of the tangent.

Theorem 1

The tangent at any point of a circle is perpendicular to the radius through the point of contacts.

Given:

A circle with centre O .

Line PQ  is tangent, touches the circle at  P.

Proof

Theorem 2

Converse of the theorem:

Given a line which is perpendicular to radius at the end point of the radius then that line is tangent to the circle.

Given:

A circle with centre O .

To Prove

XY is tangent to the circle.

Proof

Take any point Q on XY . Q is appoint other than P.

So OQ  is hypotenuse

We can say

Q is point outside the circle.

So all the points on line  XY are outside the circle.

Only point P  is on the circle.

Point of intersection of line and circle is only point  P.

Line  XY is tangent to the circle.

Theorem 3

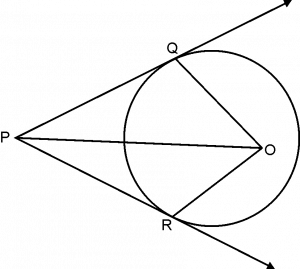
The lengths of tangents drawn from an external point to a circle are equal.

Given:

O is centre of the circle.

PQ, PR are two tangents drawn from point .

To Prove

PQ = PR

Proof

…………………..(R.H.S)

PQ = PR  ………….(CPCT)