Polynomials

Tutormate > CBSE Syllabus-Class 10th Maths > Polynomials

02 POLYNOMIALS

Degree of polynomial:The highest power of x in p(x) is called degree of the polynomial.

E g . p (x) = 3 x^{5} + 3 x^{2^{}} - 3 x + 5 h a s d e g r e e o f 5 .

Linear polynomial:The polynomial with degree 1.

E g . P (X) = 2 x + 1, 3 x + 5, \sqrt{2} x - 5, 3 x

Quadratic polynomial:The polynomial with degree 2.

E g . p (x) = 2 x^{2} + 2 x + 1, 3 x^{2} + x + 5, 2 x^{2} - \sqrt{4}, 3 x^{2}

Cubic polynomial:The polynomial with degree 3 .

E g . p (x) = 2 x^{3} + 2 x + 1, 3 x^{3} + x^{2^{}} + 1, 2 x^{3} - 5, 5 x^{3}

Value of polynomial: Value obtained by replacing by some real number k , is value of polynomial at x=k .It is denoted by .

e g . p (x) = 2 x^{2} + 2 x + 1,

p (- 2) = 2 (- 2)^{2} + 2 (- 2) + 1 = 5

value of p(x) at x=-2 =p (-2) =5

Z e r o / r o o t o f p o l y n o m i a l : I f p (k) = 0

for some k ,Kis called zero or root of polynomial.

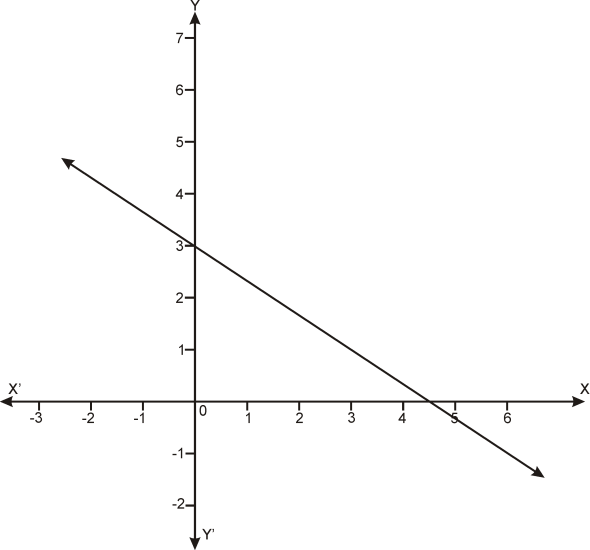
Geometrical meaning of zero:

L i n e a r p o l y n o m i a l : F o r a l i n e a r p o l y n o m i a l p (x) = a x + b

p (- b / a) = a (- b / a) + b = 0

(- b / a) i s z e r o o f t h e p o l y n o m i a l .

A n d g r a p h o f p (x) c u t s a x i s a t o n l y o n e p o i n t (- b / a, 0)

So, we say linear polynomial p(x) has only one zero, and it is the point where its graph cuts x axis

i . e x = (- b / a)

Quadratic polynomial

p (x) = a x^{2} + b x + c

Case 1):a>0 ,. graphis upward parabola .

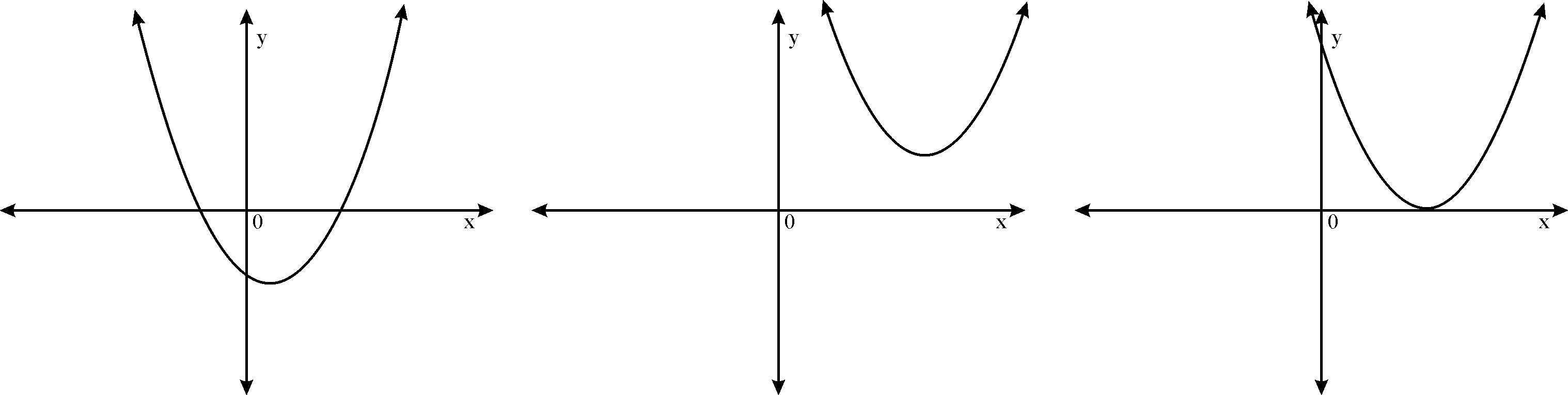
T o p r o v e : p d i v i d e s a, i . e p = k a, f o r s o m e i n t e g e r k .

Graph cuts x axis at 2 points or point or may not cut x axis.

Case 2 :a<0,The graph is downward parabola.

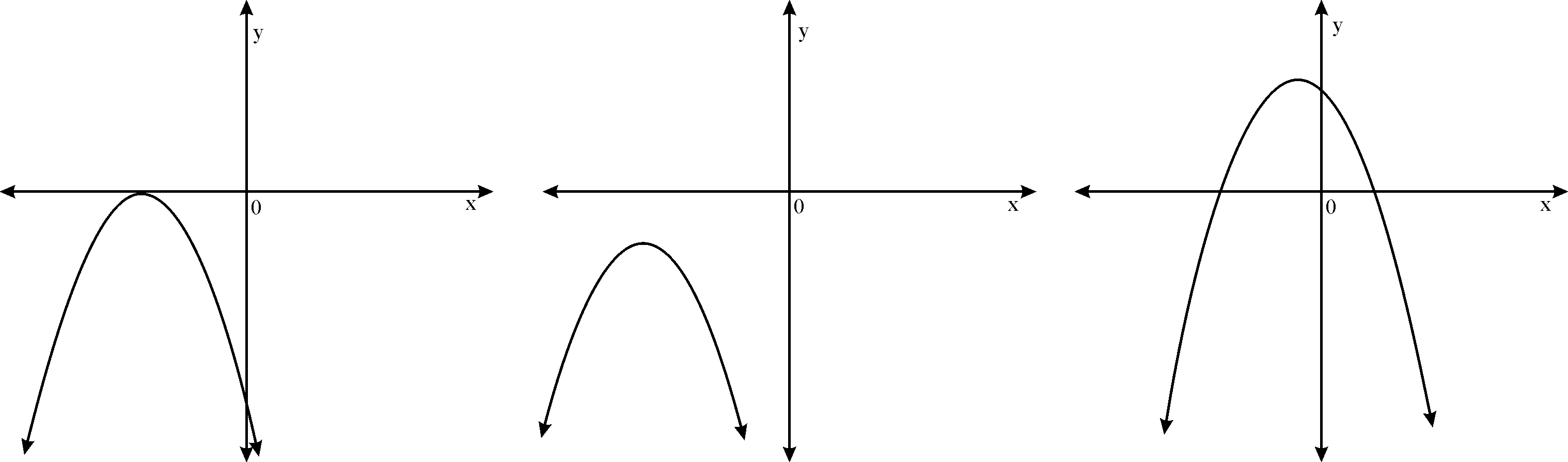
Graph cuts axis at points or point or may not cut x axis.

In either cases i) If the graph cuts x axis in two points, then we say polynomial has 2 zeroes.

ii) If the graph cuts x axis in only one point, then we say polynomial has 1 zero.

iii) If the graph does not cut x axis, then we say zeroes of polynomial do not exist.

Relation between zeroes and coefficients of polynomial:

1) Q u a d r a t i c p o l y n o m i a l : a x^{2} + b x + c

I f α, β a r e t w o r o o t s o f q u a d r a t i c p o l y n o m i a l .

s u m o f z e r o e s = \frac{- c o e f f i c i e n t o f X}{c o e f f i c i e n t o f x^{2}}

i . e . α + β = \frac{- b}{a}

p r o d u c t o f z e r o e s = \frac{c o e f f i c i e n t t e r m s}{c o e f f i c i e n t o f x^{2}}

i . e . α β = \frac{c}{a}

2) C u b i c p o l y n o m i a l : p (x) = a x^{3} + b x^{2} + c x + d

I f α, β, γ a r e t w o r o o t s o f c u b i c p o l y n o m i a l .

s u m o f z e r o e s = \frac{- c o e f f i c i e n t o f x^{2}}{c o e f f i c i e n t o f x^{3}}

α + β + γ = \frac{- b}{a}

s u m o f p r o d u c t t a k e n t w o a t a t i m e = \frac{c o e f f i c i a n t o f x}{c o e f f i c i a n t o f x^{3}}

i . e . α β + β γ + α γ = \frac{c}{a}

p r o d u c t o f z e r o e s = \frac{- c o n s \tan t t e r m s}{c o e f f i c i e n t o f x^{3}}

i . e . p r o d u c t o f z e r o e s = α β = \frac{- d}{a}

Division algorithm for polynomial:

p (x) a n d g (x) a r e t w o p o l y n o m i a l s w i t h d e g r e e o f

g (x) < d e g r e e o f p (x) t h e n p (x) = q (x) g (x) + r (x), w h e r e r (x) = 0 o r

d e g r (x) \leq d e g g (x)

Or we can express polynomial as

D i v i d e n d = Q u o t i e n t \times D i v i s o r + R e m a i n d e r

< Previous Chapter

Next Chapter >

Real Numbers

Pair of linear equation

Quadratic Equation

Arithmetic Progression

Triangles

Coordinate geometry

Introduction to trigonometry

Application of trigonometric ratio

Circles

Constructions

Areas related to circle

Surface areas and volumes

Statistics

Probability

Start your learning Journey !

Get SMS link to download the app