Coordinate geometry

X- coordinate(Abscissa) : It is the distance of a point from $\text{Y}$ axis.

Y- coordinate(Ordinate) : It is the distance of a point from $\text{X}$ axis.

Distance formula: Given points $\text{A}\left({\text{x}}_{\text{1}}{\text{, y}}_{\text{1}}\right)\text{, B}\left({\text{x}}_{\text{2}}{\text{, y}}_{\text{2}}\right)$

The distance from $\text{A}$ to $\text{B}$ is $\text{d}\left(\text{A, B}\right)\text{ = }\sqrt{{\left({\text{x}}_{\text{2}}{\text{- x}}_{\text{1}}\right)}^{\text{2}}\text{+ }{\left({\text{y}}_{\text{2}}{\text{- y}}_{\text{1}}\right)}^{\text{2}}}$

Section Formula:Given points $\text{A}\left({\text{x}}_{\text{1}}{\text{, y}}_{\text{1}}\right)\text{, B}\left({\text{x}}_{\text{2}}{\text{, y}}_{\text{2}}\right).$ if point $\text{P}\left(\text{x, y}\right)$ which divides the line segment $\text{AB}$ internally in the ratio m:n, then coordinates of points $\text{P}$ are given by

$\text{P = }\left(\frac{{\text{mx}}_{\text{2}}{\text{+ nx}}_{\text{1}}}{\text{m + n}}\text{, }\frac{{\text{my}}_{\text{2}}{\text{+ ny}}_{\text{1}}}{\text{m + n}}\right)$

Mid point formula: If P is mid point of segment AB,where $\text{A}\left({\text{x}}_{\text{1}}{\text{, y}}_{\text{1}}\right)\text{, B}\left({\text{x}}_{\text{2}}{\text{, y}}_{\text{2}}\right)$

Then $\text{P = }\left(\frac{{\text{x}}_{\text{2}}{\text{+ x}}_{\text{1}}}{\text{2}}\text{, }\frac{{\text{y}}_{\text{2}}{\text{+ y}}_{\text{1}}}{\text{2}}\right)$

Area of triangle : If $\text{A}\left({\text{x}}_{\text{1}}{\text{, y}}_{\text{1}}\right)\text{, B}\left({\text{x}}_{\text{2}}{\text{, y}}_{\text{2}}\right)\text{, C}\left({\text{x}}_{\text{3}}{\text{, y}}_{\text{3}}\right)$ are vertices of triangle then area of triangle is given by

$\frac{1}{2}\sqrt{{\text{x}}_{\text{1}}\left({\text{y}}_{\text{2}}{\text{- y}}_{\text{3}}\right){\text{ + x}}_{\text{2}}\left({\text{y}}_{\text{3}}{\text{- y}}_{\text{1}}\right){\text{ + x}}_{\text{3}}\left({\text{y}}_{\text{1}}{\text{- y}}_{\text{2}}\right)}$

* To find the area of a polygon we divide it in triangles and take numerical value of the area of each of the triangles.

* The area of $\Delta \text{ABC}$ can also be computed by using the following steps:

STEP I: Write the coordinates of the vertices $\text{A}\left({\text{x}}_{\text{1}}{\text{, y}}_{\text{1}}\right)\text{, B}\left({\text{x}}_{\text{2}}{\text{, y}}_{\text{2}}\right)$ and $\text{C}\left({\text{x}}_{\text{3}}{\text{, y}}_{\text{3}}\right)$ in three

columns as shown below and augment the coordinates of $\text{A}\left({\text{x}}_{\text{1}}{\text{, y}}_{\text{1}}\right)$ as fourth column.

STEP II:Draw broken parallel lines pointing down wards from left to right and right to left.

${\text{x}}_{\text{1}}{\text{x}}_{\text{2}}{\text{x}}_{\text{3}}{\text{x}}_{\text{1}}$

${\text{y}}_{\text{1}}{\text{y}}_{\text{2}}{\text{y}}_{\text{3}}{\text{y}}_{\text{1}}$

STEP III:Compute the sum of the products of numbers at the ends of lines pointing

downwards from left to right and subtract from this sum, the sum of the products of numbers at the ends of the lines pointing downward from right to left i.e., compute

$\left({\text{x}}_{\text{1}}{\text{y}}_{\text{2}}{\text{+ x}}_{\text{2}}{\text{y}}_{\text{3}}{\text{+ x}}_{\text{3}}{\text{y}}_{\text{1}}\right)\text{ - }\left({\text{x}}_{\text{2}}{\text{y}}_{\text{1}}{\text{+ x}}_{\text{3}}{\text{y}}_{\text{2}}{\text{+ x}}_{\text{1}}{\text{y}}_{\text{3}}\right)$

STEP IV: Find the absolute of the number obtained in step III and take its half to obtain the area.

* Three points $\text{A}\left({\text{x}}_{\text{1}}{\text{, y}}_{\text{1}}\right)\text{, B}\left({\text{x}}_{\text{2}}{\text{, y}}_{\text{2}}\right)$ and $\text{C}\left({\text{x}}_{\text{3}}{\text{, y}}_{\text{3}}\right)$ are collinear if

Area of $\text{ΔABC = 0}$ i.e., ${\text{x}}_{\text{1}}\left({\text{y}}_{\text{2}}{\text{- y}}_{\text{3}}\right){\text{ + x}}_{\text{2}}\left({\text{y}}_{\text{3}}{\text{- y}}_{\text{1}}\right){\text{ + x}}_{\text{3}}\left({\text{y}}_{\text{1}}{\text{- y}}_{\text{2}}\right)\text{ = 0}$

THEOREM 1: Prove that the coordinates of the centroid of the triangle whose vertices are

$\left({\text{x}}_{\text{1}}{\text{, y}}_{\text{1}}\right)\text{,}\left({\text{x}}_{\text{2}}{\text{, y}}_{\text{2}}\right)$ and $\left({\text{x}}_{\text{3}}{\text{, y}}_{\text{3}}\right)$ are

$\left(\frac{{\text{x}}_{\text{1}}{\text{ + x}}_{\text{2}}{\text{ + x}}_{\text{3}}}{\text{3}}\text{, }\frac{{\text{y}}_{\text{1}}{\text{ + y}}_{\text{2}}{\text{ + y}}_{\text{3}}}{\text{3}}\right)$

Also deduce that the medians of a triangle are concurrent.

[NCERT, CBSE 2004]

PROOF: Let $\text{A}\left({\text{x}}_{\text{1}}{\text{, y}}_{\text{1}}\right)\text{, B}\left({\text{x}}_{\text{2}}{\text{, y}}_{\text{2}}\right)$ and $\text{C}\left({\text{x}}_{\text{3}}{\text{, y}}_{\text{3}}\right)$ be the vertices of $\Delta \text{ABC}$ whose medians are AD, BE and $\text{CF}$ respectively. So $\text{D, E}$ and $\text{F}$ are respectively the mid-points of $\text{BC, CA}$ and $\text{AB}$.

Coordinates of $\text{D}$ are $\left(\frac{{\text{x}}_{\text{2}}{\text{ + x}}_{\text{3}}}{\text{2}}\text{, }\frac{{\text{y}}_{\text{2}}{\text{ + y}}_{\text{3}}}{\text{2}}\right)$

Coordinates of a point dividing $\text{AD}$ in the ratio $2:1$ are

$\left(\frac{{\text{1x}}_{\text{1}}\text{+ 2}\left(\frac{{\text{x}}_{\text{2}}{\text{ + x}}_{\text{3}}}{\text{2}}\right)}{\text{1 + 2}}\text{, }\frac{{\text{1y}}_{\text{1}}\text{+ 2}\left(\frac{{\text{y}}_{\text{2}}{\text{ + y}}_{\text{3}}}{\text{2}}\right)}{\text{1 + 2}}\right)\text{ = }\left(\frac{{\text{x}}_{\text{1}}{\text{ + x}}_{\text{2}}{\text{ + x}}_{\text{3}}}{\text{3}}\text{, }\frac{{\text{y}}_{\text{1}}{\text{ + y}}_{\text{2}}{\text{ + y}}_{\text{3}}}{\text{3}}\right)$

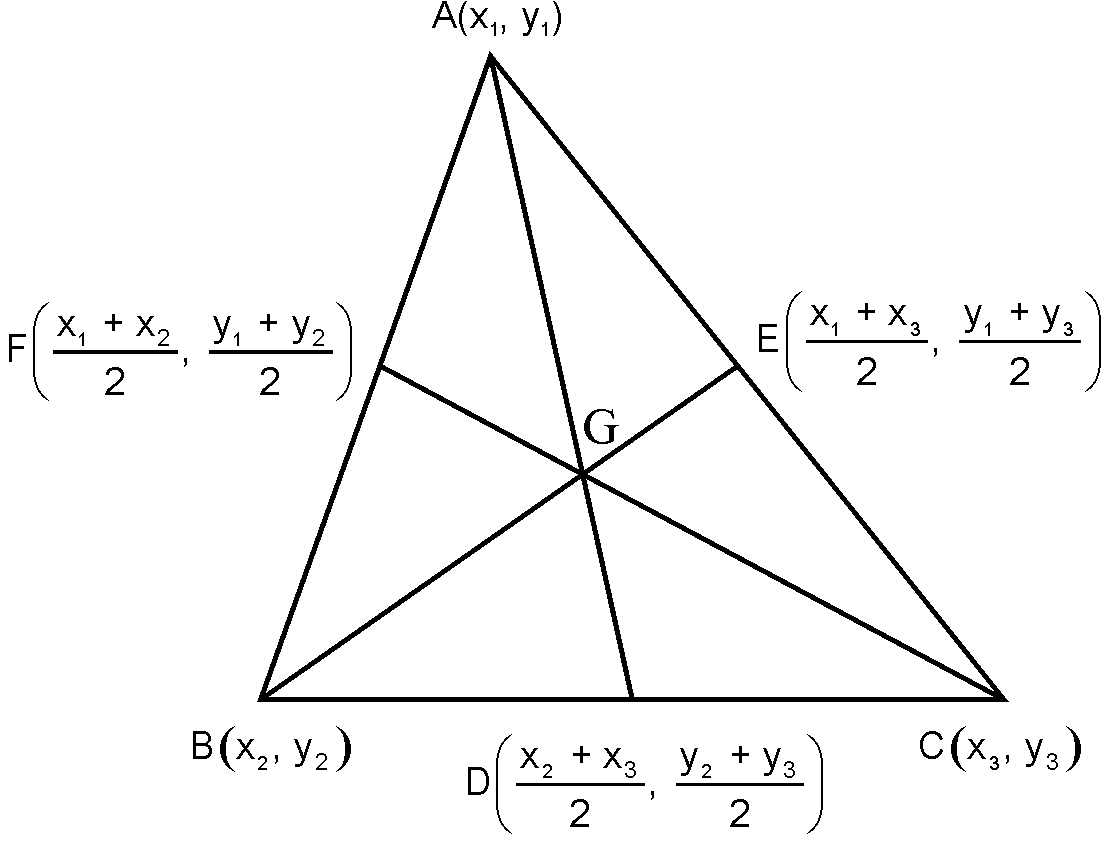
The coordinates of E are $\left(\frac{{\text{x}}_{\text{1}}{\text{ + x}}_{\text{3}}}{\text{2}}\text{, }\frac{{\text{y}}_{\text{1}}{\text{ + y}}_{\text{3}}}{\text{2}}\right)$

The coordinates of a point dividing BE in the ratio $2:1$ are

$\left(\frac{{\text{1x}}_{\text{2}}\text{+ 2}\left(\frac{{\text{x}}_{\text{1}}{\text{ + x}}_{\text{3}}}{\text{2}}\right)}{\text{1 + 2}}\text{, }\frac{{\text{1y}}_{\text{2}}\text{+ 2}\left(\frac{{\text{y}}_{\text{1}}{\text{ + y}}_{\text{3}}}{\text{2}}\right)}{\text{1 + 2}}\right)\text{ = }\left(\frac{{\text{x}}_{\text{1}}{\text{ + x}}_{\text{2}}{\text{ + x}}_{\text{3}}}{\text{3}}\text{, }\frac{{\text{y}}_{\text{1}}{\text{ + y}}_{\text{2}}{\text{ + y}}_{\text{3}}}{\text{3}}\right)$

Similarly the coordinates of a point dividing CF in the ratio $2:1$ are

$\left(\frac{{\text{x}}_{\text{1}}{\text{ + x}}_{\text{2}}{\text{ + x}}_{\text{3}}}{\text{3}}\text{, }\frac{{\text{y}}_{\text{1}}{\text{ + y}}_{\text{2}}{\text{ + y}}_{\text{3}}}{\text{3}}\right)$.

Thus, the point having coordinates $\left(\frac{{\text{x}}_{\text{1}}{\text{ + x}}_{\text{2}}{\text{ + x}}_{\text{3}}}{\text{3}}\text{, }\frac{{\text{y}}_{\text{1}}{\text{ + y}}_{\text{2}}{\text{ + y}}_{\text{3}}}{\text{3}}\right)$ is common to $\text{AD, BE}$ and $\text{CF}$ and divides them in the ratio $1:2$.

Hence, medians of a triangle are concurrent and the coordinates of the centroid are $\left(\frac{{\text{x}}_{\text{1}}{\text{ + x}}_{\text{2}}{\text{ + x}}_{\text{3}}}{\text{3}}\text{, }\frac{{\text{y}}_{\text{1}}{\text{ + y}}_{\text{2}}{\text{ + y}}_{\text{3}}}{\text{3}}\right)$

THEOREM 2:The area of a triangle, the coordinates of whose vertices are $\left({\text{x}}_{\text{1}}{\text{, y}}_{\text{1}}\right)\text{, }\left({\text{x}}_{\text{2}}{\text{, y}}_{\text{2}}\right)$ and $\left({\text{x}}_{\text{3}}{\text{, y}}_{\text{3}}\right)$ is $\frac{\text{1}}{\text{2}}\left|{\text{x}}_{\text{1}}\left({\text{y}}_{\text{2}}{\text{ - y}}_{\text{3}}\right){\text{ + x}}_{\text{2}}\left({\text{y}}_{\text{3}}{\text{ - y}}_{\text{1}}\right){\text{ + x}}_{\text{3}}\left({\text{y}}_{\text{1}}{\text{ - y}}_{\text{2}}\right)\right|$

PROOF: LET $\text{ABC}$ be a triangle whose vertices are $\text{A}\left({\text{x}}_{\text{1}}{\text{, y}}_{\text{1}}\right)\text{, B}\left({\text{x}}_{\text{2}}{\text{, y}}_{\text{2}}\right)$ and $\text{C}\left({\text{x}}_{\text{3}}{\text{, y}}_{\text{3}}\right)$. Draw $\text{AL}$,

BM and $\text{CN}$ perpendiculars from $\text{A, B, C}$ on the $\text{x -}$ axis.

Clearly, $\text{ABML, ALNC}$ and $\text{BMNC}$ are all trapeziums.

We know that

Area of trapezium $\text{= }\frac{\text{1}}{\text{2}}$ (Sum of parallel sides)(Distance between them)

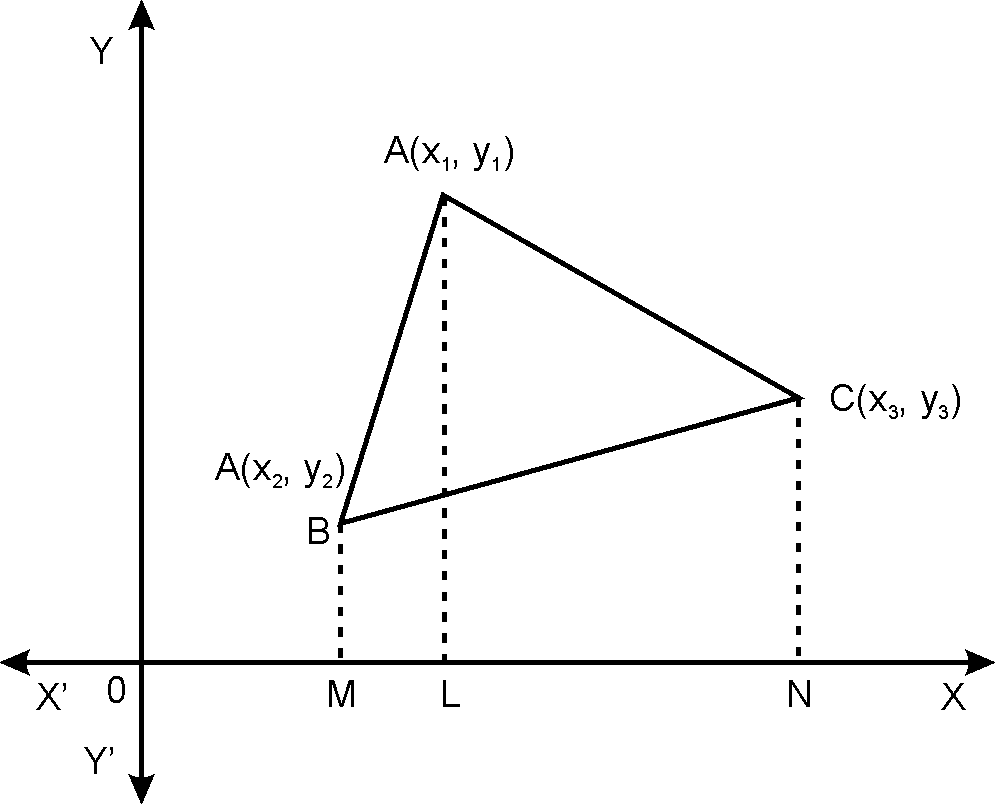
We have,

Area of $\Delta \text{ΑΒC}$ = Area of trapezium $\text{ABML +}$ Area of trapezium $\text{ALNC -}$ Area of trapezium $\text{BMNC}$ Let $\Delta$ denote the area of $\Delta \text{ΑΒC}$. Then,

$\text{Δ = }\frac{\text{1}}{\text{2}}\left(\text{BM + AL}\right)\left(\text{ML}\right)\text{ + }\frac{\text{1}}{\text{2}}\left(\text{AL + CN}\right)\left(\text{LN}\right)\text{ - }\frac{\text{1}}{\text{2}}\left(\text{BM + CN}\right)\left(\text{MN}\right)$

$\to \Delta =$

$\left|\frac{\text{1}}{\text{2}}\left({\text{y}}_{\text{2}}{\text{ + y}}_{\text{1}}\right)\left({\text{x}}_{\text{1}}{\text{ - x}}_{\text{2}}\right)\text{ + }\frac{\text{1}}{\text{2}}\left({\text{y}}_{\text{1}}{\text{ + y}}_{\text{3}}\right)\left({\text{x}}_{\text{3}}{\text{ - x}}_{\text{1}}\right)\text{ - }\frac{\text{1}}{\text{2}}\left({\text{y}}_{\text{2}}{\text{ + y}}_{\text{3}}\right)\left({\text{x}}_{\text{3}}{\text{ - x}}_{\text{2}}\right)\right|$

$\to \Delta =$

$\left|\frac{\text{1}}{\text{2}}\left\{{\text{x}}_{\text{1}}\left({\text{y}}_{\text{2}}{\text{ + y}}_{\text{1}}{\text{ - y}}_{\text{1}}{\text{ - y}}_{\text{3}}\right){\text{ + x}}_{\text{2}}\left({\text{-y}}_{\text{2}}{\text{ - y}}_{\text{1}}{\text{ + y}}_{\text{2}}{\text{ + y}}_{\text{3}}\right){\text{ + x}}_{\text{3}}\left({\text{y}}_{\text{1}}{\text{ + y}}_{\text{3}}{\text{ - y}}_{\text{2}}{\text{ - y}}_{\text{3}}\right)\right\}\right|$

$\to \text{Δ = }\frac{\text{1}}{\text{2}}\left|{\text{x}}_{\text{1}}\left({\text{y}}_{\text{2}}{\text{ - y}}_{\text{3}}\right){\text{ + x}}_{\text{2}}\left({\text{y}}_{\text{3}}{\text{ - y}}_{\text{1}}\right){\text{ + x}}_{\text{3}}\left({\text{y}}_{\text{1}}{\text{ - y}}_{\text{2}}\right)\right|$