Work and Energy

LAW OF CONSERVATION OF ENERGY

• Whenever energy changes from one form to another, the total amount of energy remains constant.
• Energy can neither be created nor destroyed.
• During the conversion of energy from one form to another, some energy may be wasted.
• The universe is an isolated system where the loss of energy in some part corresponds to a gain of an equal amount of energy in some other part of the universe. Although this principle cannot be proved, there is no known example of a violation of the law of conservation of energy.

PROOF FOR LAW OF CONSERVATION OF ENERGY:

Let a body of mass ‘m’ placed at a height ‘h’ above the ground, start falling down from rest.

In this case we have to show that the total energy (potential energy + kinetic energy) of the body A, B and C remains constant i.e, potential energy is completely transformed into kinetic energy.

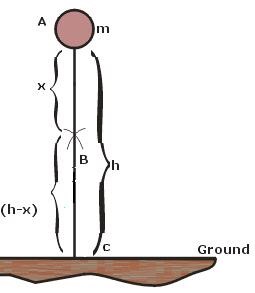
Body of mass m placed at a height h

At A,

Potential energy = m g h

Total Energy at A = Potential Energy + Kinetic Energy

= m g h  +  0

Total Energy at A = m g h ………………………………..(1)

At B,

Potential energy = m g h

= m g (h – x) [height from the ground is (h – x)]

Potential energy = m g h – m g x

The body covers the distance x with a velocity v. We make use of the third equation of motion to obtain velocity of the body.

Kinetic energy = m g x

= m g h – m g x + m g x

Total Energy at B = m g h …………………………………(2)

At C,

Potential Energy = m x g x 0

Potential energy = 0

The freely falling body has covered the distance h.

Here, u = 0,  a = g and s = h

Total energy at C = m g h………………………………(3)

It is clear from equations 1, 2 and 3 that the total energy of the body remains constant at every point. Thus, we conclude that law of conservation of energy holds good in the case of a freely falling body.

CONSERVATION OF ENERGY DURING THE FREE FALL OF A BODY

Suppose we have a ball of mass m and we raise it to a height h above the ground. As the ball falls its potential energy is gradually converted into an equal amount of kinetic energy

However, the sum of potential energy and kinetic energy of the ball remains the same at every point during its fall.

CONSERVATION OF ENERGY IN A SIMPLE PENDULUM

A swinging simple pendulum is an example of conservation of energy.

In a swinging pendulum, potential energy is transformed into kinetic energy, and the kinetic energy is transformed back into potential energy (or an oscillating simple pendulum)

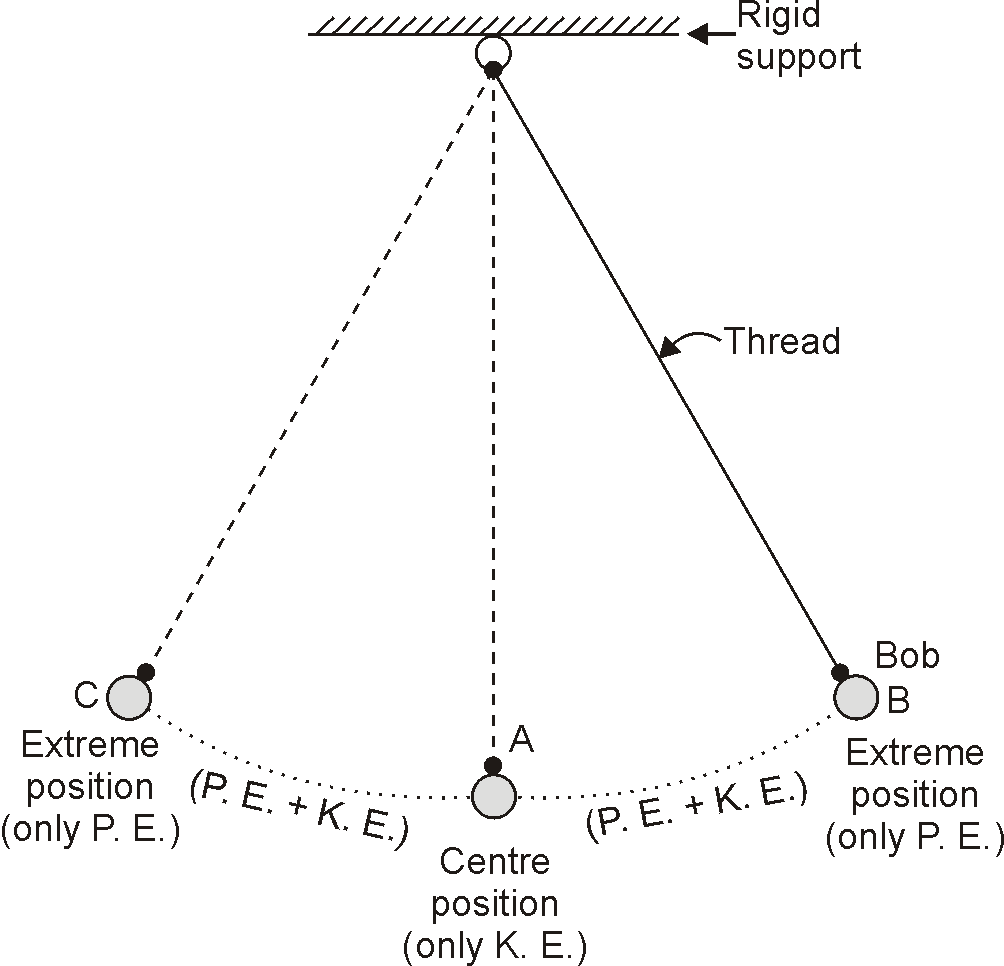
The total energy of the swinging pendulum at any instant f time remains the same (or conserved).

EXAMPLES OF LAW OF CONSERVATION:

• Electrical energy is converted into sound energy in a loudspeaker.
• The chemical energy of the batteries in a torch is converted into electrical energy, which is converted into light and heat energy.
• Chemical energy is converted into heat and light energy when fuels are burnt.
• Sound energy is converted into electrical energy in a microphone.
• Chemical energy from food is converted to thermal energy when it is broken down in the body and is used to keep it warm.
• In hydroelectric power plants, the potential energy of water is converted into the kinetic energy of the turbine, which is further converted into electrical energy. Water falls on the turbines from a height. This, in turn, rotates the turbines and generates electricity.
• Mechanical energy is converted into electrical energy in a generator.