Work and Energy

Tutormate > CBSE Syllabus-Class 9th Physics > Work and Energy

01 Work

WORK

Work is said to be done when a force acts on the body and the body moves in the direction of the force i.e. when a force produces motion.

Work done in moving a body is equal to the product of force exerted on the body and the distance moved by the body in the direction of force.

Work done = Force \times Distance

W = F \times s

When a forceis applied to a block, it moves with some acceleration. This can be proved from Newton’s Second Law of Motion

From Newton ’ s second law, F = ma . . . . . . . . . . . . . \dots . (1)

Work done = Force x Distance

W = F \times s . . . . . . . . . . . . . . . . . . . . . (2)

Substituting (2) in (1) we get:

W = (ma) . s

The speed of an object increases or decreases depending on the direction of the force.

Kinetic energyof the system changes when the force is applied.

Energy can neither be created nor be destroyed so the energy must be getting transformed into some other form. In this case that is termed as work done.

The energy decreases when negative energy is done and increases when positive work is done.

EXAMPLES OF WORK DONE

When we push a pebble lying on a surface, the pebble moves through some distance i.e. when we apply force on the pebble, the pebble gets displaced. This means that, we have done work on the pebble.
When we lift a book through a height, the book rises up. That is, work is done in moving up the book.
Then cart moves, when a bullock pulls the cart. There is a force applied on the cart, because of which the cart has moved. So, the bullock has done work on the cart.

RELATION BETWEEN KINETIC ENERGY AND WORK

Work done by (F) = Change in kinetic energy

W = \frac{1}{2} {mv}^{2} - \frac{1}{2} {mu}^{2}

W = \frac{1}{2} m - (v^{2} - u^{2})

Where u is the initial and v is the final velocity of the body

Using third equation of motion,

v^{2} - u^{2} = 2 as

W = \frac{1}{2} m (2 as)

W = m (as)

CONDITIONS FOR WORK TO BE DONE:

These two conditions need to be satisfied for work to be done:
- A force must act on the body.
- The body should be displaced in the direction of the applied force.
It is important to understand that even if either of the above two conditions is not satisfied, work is not done.

ILLUSTRATIONS OF NO WORK

EXAMPLE 1:

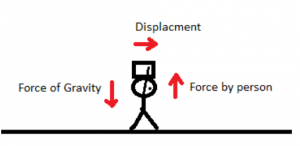
Consider the example of a boy carrying luggage. The force acting on the luggage is the force of gravity, which is vertical and displacement is horizontal. So the displacement in the direction of the force is zero, hence work done by gravity as well as the person is zero.

EXAMPLE 2:

When we push a wall, even though we feel fatigue but work done by on the wall is zero. This is because displacement of the wall is zero. So according to the formula,

W = F.s

W = F.0

W = 0

UNIT OF WORK

The SI unit of work is newton metre, which is denoted as Nm or joule denoted as J.
Work is a scalar quantity.
One joule of work is said to be done, whenever a force of one newton displaces a body through a distance of 1 metre in its own direction

$1 Joule = 1 Newton \times 1 metre$

$1 J = 1 Nm$

WORK DONE AGAINST GRAVITY

Work done in lifting a body = Weight of a body x Vertical distance

W = m x g x h

MEASUREMENT OF WORK

When a force F acts along the direction of motion of the body,

Work done = Force x Distance

W = F . s

When force F makes an angle 0 with the displacement s of the body,

W = F s \cos (θ)

For maximum work, θ = 0^{\circ} .

For minimum work, θ = 90^{\circ} .

Work done on an object by a force would be zero if the displacement of the object is zero.

POSITIVE, NEGATIVE AND ZERO WORK

The work done by a force can be positive, negative or zero.

Work done is positive when a force acts in the direction of the displacement.
Work done is negative when a force acts opposite to the direction of the displacement.
Work done is zero when a force acts at right angles to the direction of the displacement.