Motion

05 Average and Instantaneous Acceleration

Average acceleration over a period of time is defined as the total change in velocity in the given interval divided by the total time taken for the change.
For a given interval of time, it is denoted as
$\bar{a}$
.

\bar{a} = \frac{v_{2} - v_{1}}{t_{2} - t_{1}} = \frac{∆ v}{∆ t}

Mathematically,
$\bar{a} = \frac{v_{2} - v_{1}}{t_{2} - t_{1}} = \frac{∆ v}{∆ t}$
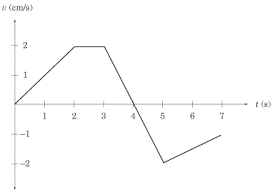
Whereandare the instantaneous velocities at timeandandis the average acceleration.
In the velocity time graph shown above, the slope of the line between any time interval t₁ and t₂ gives the average value for the rate of change of velocity for the object during the time t₁ and t₂

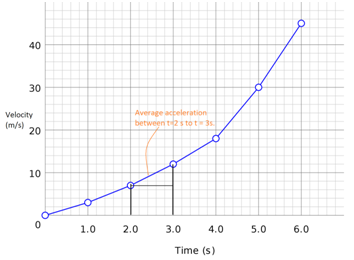
In a velocity-time curve, the instantaneous acceleration is given by the slope of the tangent on the curve at any instant.

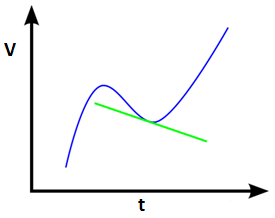
Consider the velocity-time graph shown below:

Here, between the time intervals of 0 – 2 seconds, the velocity of the particle is increasing with respect to time. In other words, the slope of the v -t curve in this time interval is positive. So it experiences a positive acceleration.
Between the time intervals of 2 – 3 seconds, the velocity of the object is constant with respect to time. slope of the v -t curve in this time interval is 0. So, the body experiences zero acceleration.
Consider the time intervals between 3 – 5 seconds. The velocity of the body decreases with respect to time. In other words, the slope of the v -t curve in this time interval is negative. So, the body experiences a negative value of acceleration.