Combination of resistors: series and parallel

Tutormate > CBSE Syllabus-Class 10th Physics > Combination of resistors: series and parallel

03 Electricity

COMBINATION OR A SYSTEM OF RESISTANCES (OR RESISTORS)

The resistance can be combined in two ways:

(i) In series, and

(ii) In parallel.

In Series: When two (or more) resistances are connected end to end consecutively, they are said to be connected in series.

In Parallel: When two (or more) resistances are connected between the same two points, they are said to be connected in parallel.

RESISTANCES (OR RESISTORS) IN SERIES

When two or more resistances are joined end to end so that same current flows through each of them in turn, they are said to be connected in series. Here, the total resistance is equal to the sum of the individual resistances.

C o n s i d e r, r e s i s \tan c e s R_{1} R_{2} R_{3} \dots . T h e y a r e c o n n e c t e d i n s e r i e s . T h e n t h e i r c o m b i n e d r e s i s \tan c e R i s g i v e n b y : R_{s} = R_{1} + R_{2} + R_{3} + . . .

Resultant Resistance of Two Resistances Connected in Series

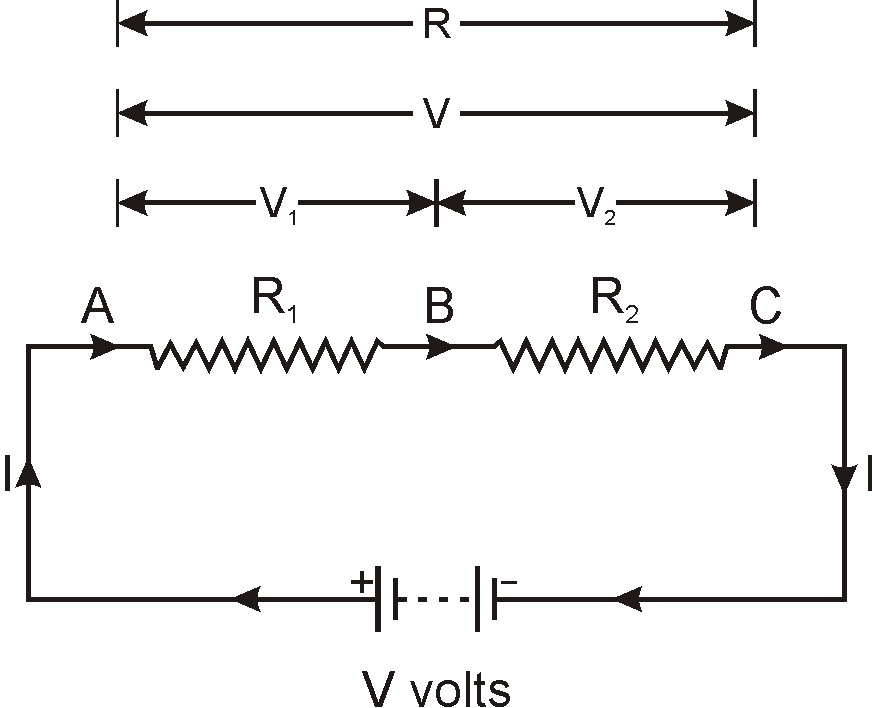
C o n s i d e r t w o r e s i s \tan c e s a n d c o n n e c t e d i n s e r i e s R_{1} a n d R_{2} . A b a t t e r y o f V v o l t s h a s b e e n a p p l i e d t o t h e e n d s o f t h i s s e r i e s c o m b i n a t i o n . N o w, s u p p o s e t h e p o t e n t i a l d i f f e r e n c e a c r o s s t h e r e s i s \tan c e R_{1} i s V_{1} a n d t h e p o t e n t i a l d i f f e r e n c e a c r o s s t h e r e s i s \tan c e R_{2} i s V_{2} . W e h a v e a p p l i e d a b a t t e r y o f v o l t a g e V, s o t h e t o t a l p o t e n t i a l d i f f e r e n c e a c r o s s t h e t w o r e s i s \tan c e s s h o u l d b e e q u a l t o t h e v o l t a g e o f t h e b a t t e r y .

T h a t i s : V = V_{1} + V_{2} \dots (1)

So, applying Ohm’s law to the whole circuit, we get:

\frac{V}{I} = R

O r V = I \times R . . . (2)

V_{1} = I \times R_{1} . . . (3)

A n d V_{2} = I \times R_{2} . . . (4)

Cancelling I from both sides, we get:

Resultant resistance (combined resistance or equivalent resistance),

R = R_{1} + R_{2}

RESISTANCES (OR RESISTORS) IN PARALLEL

When two or more resistances are connected across two points so that each of them provides a separate path for current, they are said to be connected in parallel.
Here the reciprocal of their combined resistance is equal to the sum of the reciprocals of the individual resistances.
$F o r e x a m p l e, i f a n u m b e r o f r e s i s \tan c e s, R_{1}, R_{2}, R_{3} \dots . e t c ., a r e c o n n e c t e d i n p a r a l l e l, t h e n t h e i r c o m b i n e d r e s i s \tan c e R i s g i v e n b y t h e f o r m u l a : \frac{1}{R_{p}} = \frac{1}{R_{1}} + \frac{1}{R_{2}} + \frac{1}{R_{3}} + . . .$

Combined Resistance of Two Resistances Connected in Parallel

C o n s i d e r, t w o r e s i s \tan c e s R_{1} a n d R_{2} a r e c o n n e c t e d p a r a l l e l t o o n e a n o t h e r b e t w e e n t h e s a m e t w o p o i n t s A a n d B . A b a t t e r y o f V v o l t s h a s b e e n a p p l i e d a c r o s s t h e e n d s o f t h i s c o m b i n a t i o n .

T o t a l c u r r e n t, I = I_{1} + I_{2} \dots (1)

I = \frac{V}{R} . . . (2)

I_{1} = \frac{V}{R_{1}} . . . (3)

A n d I_{2} = \frac{V}{R_{2}} . . . (4)

\frac{V}{R} = \frac{V}{R_{1}} + \frac{V}{R_{2}}

V [\frac{1}{R}] = V [\frac{1}{R_{1}} + \frac{1}{R_{2}}]

\frac{1}{R} = \frac{1}{R_{1}} + \frac{1}{R_{2_{}}}

DOMESTIC ELECTRIC CIRCUITS: SERIES OR PARALLEL

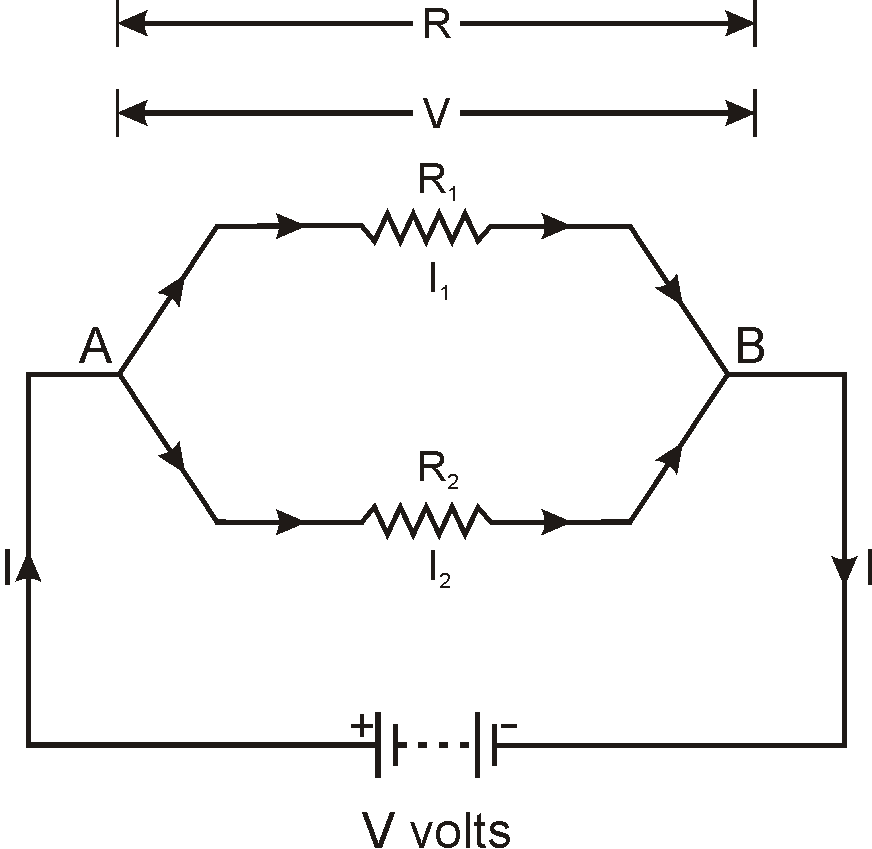
When designing an electric circuit, we should consider whether a series circuit or a parallel circuit is better for the intended use. A series circuit is also safer because the current in it is smaller.

DISADVANTAGE OF SERIES CIRCUITS FOR DOMESTIC WIRING

In series circuit, if one electrical appliance stops working due to some defect, then all other appliances also stop working.
In series circuit, all the electrical appliances have only one switch due to which they cannot be turned on or off separately.
In series circuit, the appliances do not get the same voltage (220 V) as that of the power supply line.
In the series connection of electrical appliances, the overall resistance of the circuit increases too much due to which the current from the power supply is low.

ADVANTAGES OF PARALLEL CIRCUITS IN DOMESTIC WIRING

In parallel circuits, if one electrical appliance stops working due to some defect, then all other appliances keep working normally.
In parallel circuits, each electrical appliance has its own switch due to which it can be turned on or turned off independently, without affecting other appliances.
In parallel circuits, each electrical appliance gets the same voltage (220 V) as that of the power supply line.
In the parallel connection of electrical appliance, the overall resistance of the household circuit is reduced due to which the current from the power supply is high.