Force and Laws of Motion

NEWTON’S SECOND LAW OF MOTION

• Newton’s second law of motion states that: The rate of change of momentum of a body is directly proportional to the applied force, and takes place in the direction in which the force acts.
• Newton’s second law of motion gives us a relationship between ‘force’ and ’acceleration’.
• It also gives us a method of measuring the force in terms of mass and acceleration.
• In addition to mass, velocity also affects the impact produced by any object.
• The impact produced by an object depends on its mass and velocity i.e., its momentum and the time rate at which the change in momentum is occurring. This phenomenon is validated using second law of motion.

MATHEMATICAL FORMULATION OF THE SECOND LAW OF MOTION

Let us consider an object of mass m, moving along a straight line with an initial velocity u.

Let us say, after a certain time t, with a constant acceleration, the final velocity becomes v.

As we know, the rate of change of momentum with respect to time is proportional to the applied force.

UNIT OF FORCE

The Si unit of force is newton. A newton is that force which when acting on a body of mass 1 kg produces an acceleration of

in it.

SOME APPLICATIONS OF NEWTON’S SECOND LAW OF MOTION

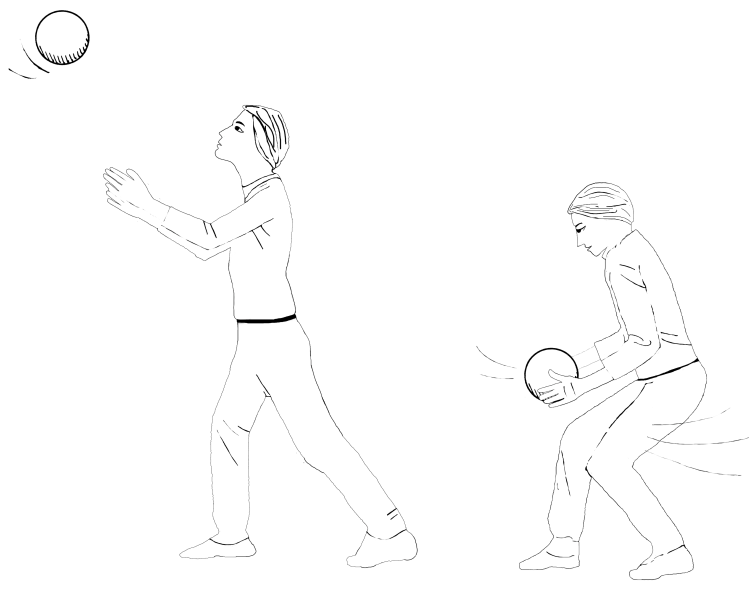
Catching a Cricket Ball

In order to catch a fast cricket ball, cricket players (or fielders), tend to move their hands backwards. This is done to prevent any injury to the hands. Because, A fast moving cricket ball has a large momentum and to stop (or catch) this cricket ball, its momentum has to be reduced to zero. Now, when a cricket player moves back his hands to catch the fast ball,   the time taken to reduce the momentum of a ball to zero is increased. As more time is taken to stop the ball, the rate of change of momentum of the ball is decreased and a small force is exerted on the hands of player. Hence the hands of the players do not get hurt while catching a fast moving ball. 

The Case of a High Jumper

During athletics meet, a high jumping athelete is provide either a cushion or a heap of sand on the ground to fall upon.

The Use of Seat Belts in Cars

All the cars are provided with seat belts for passengers these days. This is to prevent injuries in case of an accident.

EXAMPLES OF SECOND LAW OF MOTION

• A small bullet when at rest does not harm the person handling it whereas when loaded in a gun and fired with high velocity, it can kill a person.

• When a car is given a momentary jerk, it may not move from its initial position whereas when an extended and continuous force of the same magnitude is applied on the car, it experiences a displacement.

• When two same forces are applied to push a car and a bus, the car will have more acceleration compared to the bus.

• If same magnitude of force is used to push two blocks of iron, where one of the blocks is heavier than the other, the rate of change of position of the lighter block will be more than the heavier one.